10. LR(1) 파서, LALR 파서 (충남대 컴파일러 개론 강의록)

충남대학교 컴퓨터공학과 조은선 교수님의 "컴파일러 개론" 강의를 필기한 내용입니다.

다소 잘못된 내용과 구어적 표현 이 포함되어 있을 수 있습니다.

SLR의 문제점

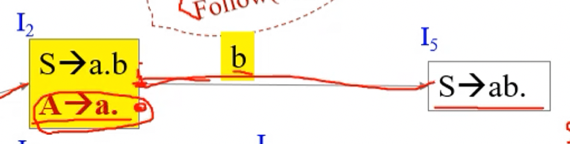
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image1.png

위 그림을 보면
i2상태에 Reduce item과 Kernel item이 같이 존재하는데 그럼 이때에는
A → a로 reduce를 해야할지 shift b를 하고 5번 상태로 갈지 알 수 없다
즉 지금까지 봐온 예제에는 Kernel item이 reduce item이어서 별 문제가 없었지만 위 예제에서 보다시피 SLR으로 해도 Shift-reduce conflict를 피할 수 없더라

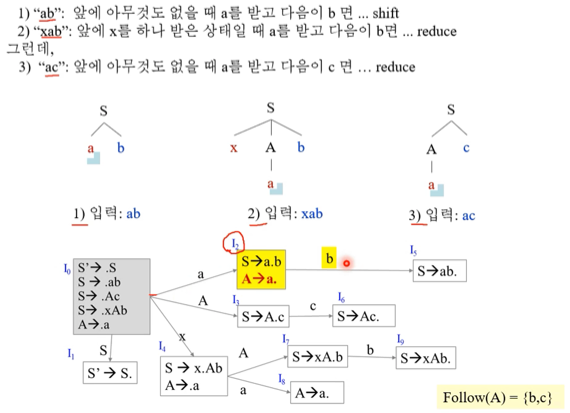
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image2.png

일단 위 그림만 보고 대강 진행과정을 생각할 수 있어야 한다
그림만 보고 할때는 Reduce를 하면 왔던대로 다시 갔다가 Reduce해서 생긴 논터미널로 움직여줘야되는것 잊지말
어쨋든 위의 예제에서 보면
ab같은 경우에는 2번에서 shift b를 하고 5번으로 가야되고
ac같은 경우에는 2번에서 Reduce A → a를 하고 0번으로 갔다가 3번으로 가야된다
하지만 2번에서는 A의 Follow에 b와 c가 모두 있기 때문에 SLR가지고는 위와같은 세밀한 컨트롤이 안된다 이거임

LR(1) Parsing

이것을 해결하고자 그냥 Follow가 아니라 그 path를 타고 왔을때 Follow는 누구냐? 이 뭔소리여
어쨋든 그냥 Follow가 아니라 좀 더 조건을 세분화할 필요가 있는 것
따라서 LR(1) Item을 좀 변형해 해당 생성규칙으로 Reduce되었을 때 다음에 나와야 되는 토큰도 같이 명시하게 된다
이제는 그냥 Reduce를 하는게 아니라 그 다음에 나오는 토큰(Lookahead라고 부름)까지 확인을 하고 Reduce를 하는거고 따라서 그 다음 토큰 하나를 더 확인하기 때문에 LR(1) 이 되는거다
- LL에서의 Lookahead와의 차이점은 LL(1)이면 그다음 토큰 하나를 보고 다음 액션을 결정해주는 것이었다면
- LR(1)은 그 다음 토큰 하나를 보고 테이블을 만들겠다는 약간의 의미상으로 차이가 있다

LR(1) Item

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image3.png

일단 LR(0) Item과의 차이점은 맨 뒤에 콤마(,)를 찍고 해당 생성규칙으로 Reduce를 한 다음에 기대하는 토큰이 명시되게 된다는 점이다
- 즉, LHS도 Reduce한 다음에 나올 토큰이기 때문에 SLR처럼 Follow를 고려해주는 셈이지만 SLR에서는 모든 Follow 원소에 대해 Reduce를 하는 것이었다면 여기서는 이제 Follow원소 중 부분집합에 대해서의 액션을 좀 더 세분화해서 명시하게 되는 것
따라서 위의 식의 의미를 생각해보면 X → a.b에서 b가 나오면 X → ab.가 되므로 reduce를 해야하지만 reduce를 한 다음에 y가 등장해야만 reduce를 하라는 의미가 되는 것

LR(1) Closure, goto

LR(1) Item이라는게 새로 확장되었으므로 LR(1) Closure도 확장해줘야 한다
그리고 goto의 경우에도 점을 이동하고 Closure를 해주는 것은 동일하지만 Closure가 바뀌었기 때문에 조금 달라지게 되는 것

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image4.png

일단 시작상태의 Augment grammar가 위처럼 $가 Lookahead로 추가된 것으로 바뀐다

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image5.png

Closure의 진행과정을 보면
일단 점 뒤에 터미널이 오면 끝나는건 매한가지이다
그리고 점 뒤에 논터미널이 있으면 그 논터미널에 대한 생성규칙에 점찍어서 갖고오고 재귀적으로 Closure을 구해줘야 하는 것도 동일하다
근데 달라지는 것은
이제 LR(1) Item의 경우에는 Lookahead까지 같이 계산해서 명시해야 하기 때문에 추가적인 연산이 더 들어감
어케하냐면 점 뒤에 논터미널인 경우에는 해당 논터미널을 갖고 오되 논터미널 뒤로 점이 움직였을 경우 등장할 수 있는 토큰들을 Lookahead로 넣어주면 된다
- 위의 예제에서 보면 [S’ → .S , $] 에서 일단 S에 대한 생성규칙을 다 갖고와 점을 찍어준다 - 즉, [S → .E+S] 와 [S → .E]
- 그리고 [S’ → .S , $] 에서 S뒤로 점이 이동했을 때 나올 수 있는 것은 $밖에 없으므로 Closure Item에 대해서도 $를 Lookahead로 추가해준다 - 즉, [S → .E+S , $] 와 [S → .E , $]
- 그리고 확장된 애들에 대해서도 Closure를 해주기 위해 점 뒤에 있는 E에 대한 생성규칙도 다 가져온다 - [E → .num]
- 근데 [S → .E+S , $] 와 [S → .E , $] 에서 보면 E 뒤에는 $말고도 +도 올 수 있으므로 [E → .num] 의 Lookahead로 + / $가 들어가게 되는 것이다 - 즉, [E → .num , + / $] 가 되는 것

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image6.png

goto 예제이다 - LR(0)와 동일한데 Closure이 변경되면서 그에대한 여파로 달라지게 된 것

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image7.png

풀어봐라

상태전이도

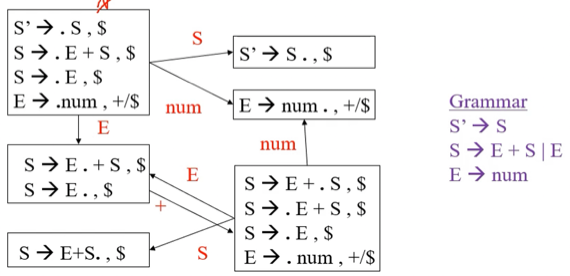
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image8.png

뭐 LR(0)에서처럼 그려주면 된다
LR(0)에서의 상태전이도가 C0였듯이 LR(1)에서의 상태전이도는 C1라고 부른다

파싱 테이블 만들기

파싱 테이블 만드는 것도 LR(0)와 거의 동일한데
Reduce Item을 처리할때는 그냥 전부 Reduce로 꼬라박는게 아니고 Lookahead에 포함된 토큰에 대해서만 Reduce를 박아주면 된다

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image9.png

빨간색 부분 처리할때 이래해주면 된다는거임

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image10.png

풀어봐라

LALR Parsing

LR(1) 파싱의 단점

얘는 이제 문제가 너무 정교해서 상태의 갯수가 너무 많아진다는 것이다
따라서 상태의 갯수는 줄이고 거의 동일한 성능을 가지는 LALR이 등장하게 되는 것

상태 갯수 줄이기

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image11.png

일단 LR(1) Item에서 Lookahead를 빼고 그 앞부분을 Core라고 하는데
두 상태의 원소가 Lookahead만 다르고 Core은 같다면 이것을 합쳐서 하나의 상태로 만든 것이 LALR이다

LALR 만들기

뭐 LR(1)을 만든 다음에 상태들을 병합할 수도 있지만 이방법은 조따 복잡하기 때문에 안쓰고
SLR을 만들어 LR(0)와 C0를 다 만들고 shift, accept, goto는 동일하지만 Reduce Item을 처리해 Reduce를 할때만 Lookahead를 고려하여 액션을 구성하게 된다

총정리

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image12.png

어떤 문법이 ~라는 것은 ~테이블에 conflict가 없다는 것이다

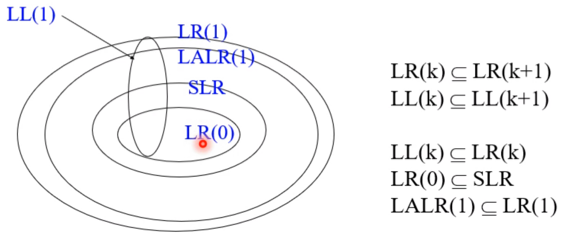
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image13.png

참고로 문법들간의 표현범위는 다음과 같음
문법을 정교하게 만들면 컴파일러가 할게 많지 않고 문법을 대충만들면 컴파일러가 수정해야되니까 할게 많더라

기출문제

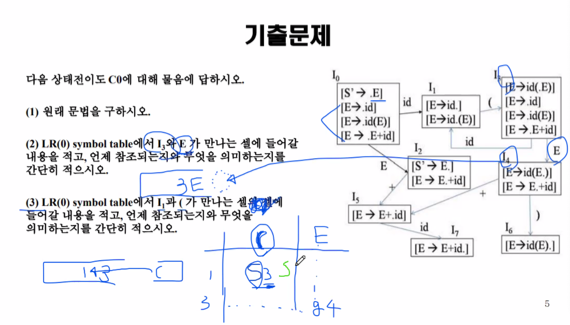
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB10%20-%20LR(1)%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5,%20LALR%20%E1%84%91%E1%85%A1%E1%84%89%E1%85%A5%204dcc5173e9d6479dae94c73ca785c07d/image14.png

2, 3번문항 스택과 입력스트링 그려서 설명하라

Madison Digital Garden

10. LR(1) 파서, LALR 파서 (충남대 컴파일러 개론 강의록)

SLR의 문제점