Madison Digital Garden

Search

SearchSearch

4. Top-down 구문분석 (충남대 컴파일러 개론 강의록)

Sep 25, 2021, 13 min read

충남대학교 컴퓨터공학과 조은선 교수님의 "컴파일러 개론" 강의를 필기한 내용입니다.

다소 잘못된 내용과 구어적 표현 이 포함되어 있을 수 있습니다.

Top-down 구문분석

  • 시작심벌부터 시작해 가능한 좌측 유도를 다 해보는 것
  • 물론 전부 다 하는건 아니고 하나씩 맞춰보면서 한다
    • a가 들어왔으면 a로 시작하는 생성규칙 중 첫번째꺼부터 해보는 것
  • 매치되는 생성규칙이 없을 떄 Backtracking 을 함
    • 바로 직전의 생성규칙을 롤백시키고, 토큰도 다시 Stream에 넣어주고 다른 생성규칙을 시도
    • 따라서 Backtracking의 오버헤드는 매우 클 수도 있다
  • 더이상 적용할 생성규칙이 없으면 틀린것으로 인식

예제

  • accd에 대해 Top-down방식으로 구문분석을 하면

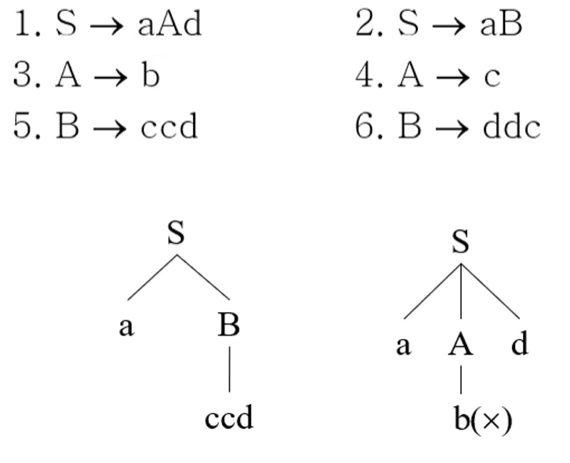
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image1.png

  • 일단 시작심벌에서 a로 시작하는 규칙이 두개 있으므로 1번부터 해봄
  • 그다음에는 c로 시작하는 규칙이 4번이므로 4번을 적용
  • 논터미널이 더이상 없는데 매칭되지 않으므로 4번을 롤백, 3번을 골라도 안되므로 백트래킹 - 1번를 롤백하고 2번 적용
  • 2번을 적용한 뒤 c로 시작하는것이 5번 규칙이므로 5번을 적용
  • 적용후에 논터미널이 더이상 없고, 매치되므로 문법을 준수한다고 판단

LL파싱

  • 일단 Left-to right, 즉, 왼쪽에서 오른쪽으로 읽어나가며 파싱한다
  • 결과적으로 Left Parse 즉, 좌파스가 생성되게 된다
  • 또한 LL파싱의 제일 중요한 특징은 Deterministic Parsing 이다
    • 입력 문자가 하나 들어오면 해당 입력문자에 적용될 수 있는 생성규칙은 하나여야 된다는 것
    • 예를 들면 위의 예제에는 S → aAd와 S → aB가 있으므로 a가 들어왔을 때 생성규칙이 두개가 가능하다
      • 이러한 경우에 Deterministic 하지 않다라고 하는 것
  • 입력문자와 생성 터미널이 다르면 백트래킹 안하고 걍 틀린것으로 간주 - 백트래킹을 안한다는 장점이 있지만
  • 결정적이지 않은 경우에는 걍 파싱을 안한다 - 즉, 파싱할 수 있는 범위가 좁다는 단점이 있다
  • 따라서 LL파싱은 조금이라도 결정적으로 파싱이 될 수 있는 가능성이 있는 문법만을 받아 결정적이지 않은 곳은 다듬어서 사용하고
  • 입력문자당 적용될 생성규칙을 key-value쌍으로 미리 뽑아두고 파싱하게 된다.
  • 따라서 규칙을 보고 필요한 정보가 무엇인지 모으는 작업을 하게 된다
  • 이때 정보라는 것은 일련의 집합이며 FIRST, FOLLOW , LOOKAHEAD 등등이 존재한다

FIRST

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image2.png

  • Nonterminal A로부터 유도될 수 있는 모든 것들 중 맨 먼저 나올 수 있는 terminal들의 집합이다
  • 아래 예제 보면 딱이해됨

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image3.png

  • S로 유도되는 문자열은 무조건 a로 시작하므로 FIRST(S)는 {a}
  • A로 유도되는 문자열은 무조건 b아니면 c로 시작하므로 FIRST(A)는 {b, c}
  • B로 유도되는 문자열은 무조건 c아니면 d로 시작하므로 FIRST(B)는 {c, d}인 셈
  • 만약에 S → Abe가 추가된다면 FIRST(A)가 {b, c}였기 때문에 S로 유도되는 문자열은 b나 c로 시작할 수도 있게 됨 - 따라서 FIRST(S)는 {a, b, c}가 된다

FIRST 계산하는 방법

  • 일단 e-생성규칙(여기서 e는 입실론, 즉, 널을 의미함)은 X → e의 형태를 의미한다
  • 그리고 Nullable nonterminal은 Nonterminal A가 e로 유도될 수 있을 때를 의미함 - 이렇게되면 A는 사라져벌이는 것
  • LHS, RHS는 뭔지 알제? 생성규칙의 화살표 기준으로 왼쪽에 있는놈이랑 오른쪽에 있는 놈
  • Ring Sum은 아래 보면 딱 안다

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image4.png

  • 즉, 먼저등장하는놈에 널이 없으면 뒤에꺼는 걍 무시
  • 널이 있으면 앞에놈에서 널을 빼고 뒤에꺼랑 합집합

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image5.png

  • FIRST를 계산하는 규칙은 위와 같다
  • 뭐 1, 2, 3번은 걍 개껌이고
  • 4번을 좀 잘 봐야되는데 4번에서 = 오른쪽에 있는 FIRST(X)는 1, 2, 3번을 통해 구해낸 FIRST(X)를 의미한다
  • 그리고 여기다가 Y1부터 Yk까지를 RingSum해서 합집합을 해주면 됨
  • 이짓을 모든 Nonterminal의 FIRST가 변하지 않을 때까지 반복한다는데 이건 뒤에 가면 이해될거임

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image6.png

  • 위의 예제를 보면
  • FIRST(S)를 구할 때 일단 S → Ab는 제쳐두고 두세번째 규칙을 보면
  • 일단 두번째 식으로 F(S) = {c}이고 세번째 식으로 F(A) = {e}임
  • 첫번째 식을 처리하기 위해 F(Ab) 를 뜯어보면
  • 이건 F(A) (+) F(b)이기 때문에 {e} (+) {b}가 되고 따라서 {b}가 된다
  • 이것을 두번째 식으로 구한 {c}와 합집합해주면 {b, c}가 되는 것
  • 따라서 S에서 b나 c가 들어오면 정상이지만 그렇지 않으면 오류를 출력하면 되는 것이다

예제들

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image7.png

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image8.png

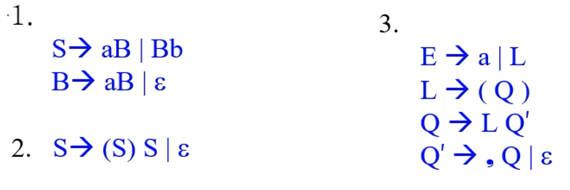
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image9.png

  • 이거 반드시 시험에 나오니까 그냥 과정 자체를 외워버려라
    1. 일단 모든 Nonterminal에 대한 FIRST들을 공집합으로 두고
    2. 1, 2, 3번 규칙으로 가능한 Nonterminal들에 대해 FIRST들을 갱신한다
    3. 그리고 4번 규칙을 이용해 가능한 Nonterminal들에 대해 FIRST들을 갱신하고
    4. 갱신한 것들을 가지고 다시한번 4번 규칙을 적용해 갱신해본다
    5. 만약 갱신되지 않는다면, 완료

FOLLOW

  • FIRST의 문제점 : Non-terminal이 Nullable한 상황에서는 FIRST만을 구하는 것으로는 한계가 있음

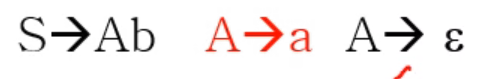
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image10.png

  • 이 예시를 보면 딱 이해된다
  • 만약에 b가 들어오면 세번째 놈을 선택하면 된다는 것을 우리는 딱 보면 알 수 있다
  • 컴퓨터 입장에서도 FIRST(S)가 {a, b}이기 때문에 b가 들어오면 구문분석이 가능하다는 것을 깨닫고 첫번째를 선택할 것이다
  • 하지만 선택하고 난 뒤에는 FIRST(A)가 {a, e}이기 때문에 b를 만들 수 없다고 판단하게 되는것
  • 즉, 이론적으로는 가능한 상황임에도 FIRST만 생각하면 로직때문에 구문분석이 안되는 경우가 생기더라
  • 따라서 FOLLOW는 이러한 경우를 대비해 Nonterminal의 바로 뒤에 나오는 terminal들을 모은 집합이 되는 것

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image11.png

  • 뭐 결과적으로 따져보면 Non-terminal 뒤에 나오는 모든 terminal의 집합이라는 말이나 같다
  • FIRST를 구하기 위해서는 해당 Non-terminal이 LHS에 등장하는 경우를 중점적으로 봤다면,
  • FOLLOW를 구하기 위해서는 해당 Non-terminal이 RHS에 등장하는 경우를 중점적으로 살피게 된다 - 바로 뒤에 나오는 terminal들을 살피기 위해

FOLLOW를 구하는 방법

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image12.png

  • 일단. 시작심벌은 EOF를 뜻하는 $를 초기값으로 가진다 - Non-terminal뒤에 EOF이 나와도 문제가 없기 때문
  • 2번은 우리가 구하고자 하는 Non-terminal 뒤에 나오는 놈이 nullable하지 않다면, 바로 뒤에 나오는 놈의 FIRST를 추가해주면 된다는 말이다
    • 이것도 당연한 말이쥬? 바로 뒤에 null이 안나오면 바로 뒤에 있는 놈의 FIRST가 나 자신의 FOLLOW가 될 수 있는 것이니께

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image13.png

  • 얘는 우리가 구하고자 하는 Non-terminal이 생성규칙의 마지막에 있거나, 아니면 마지막에 있지는 않지만 그 뒤에 바로 나오는 놈이 Nullable하다면 해당 생성규칙의 LHS에 있는 놈의 FOLLOW도 넣어주라 이말이야
  • 얘도 좀만 생각해보면 당연한 말이다 - 만약에 Non-terminal이 시작심볼이면 이놈 뒤에 연달아 나오는 놈은 없으니까 생각할 필요가 없지만
  • 만약 S → Ab, A → cB인 경우에 B의 FOLLOW를 구한다면 B뒤에는 첫번째 생성규칙에 따라 b가 올 수 있으므로 LHS인 A의 FOLLOW인 b도 추가해줘야 된다는 것이다
  • 따라서 만약 A → xB, B → xA형태의 경우에는 첫번쨰 생성규칙으로는 B의 FOLLOW는 A의 FOLLOW를 포함하고, 두번째 생성규칙으로는 A의 FOLLOW는 B의 FOLLOW를 포함하게 되므로 이 둘은 동치가 된다
  • 그리고 FIRST에서마냥 FOLLOW를 구할때도 FOLLOW를 계속 갱신해가며 더이상 갱신이 안될때까지 3번규칙을 반복해주면 된다

예제들

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image14.png

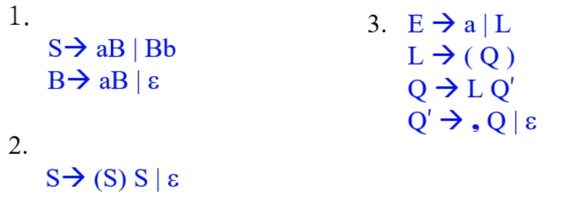
%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image15.png

%E1%84%8B%E1%85%B5%E1%84%85%E1%85%A9%E1%86%AB04%20-%20Top-down%20%E1%84%80%E1%85%AE%E1%84%86%E1%85%AE%E1%86%AB%E1%84%87%E1%85%AE%E1%86%AB%E1%84%89%E1%85%A5%E1%86%A8%2038f708ad66a9425fb468e9630413926c/image16.png

  • 얘도 순서를 위의풀이 거의 그대로 외워놓아라
    1. 전부 {}로 세팅
    2. 시작심벌을 {$}로 세팅
    3. 뒤에 뭔가 나오는 경우 그놈의 FIRST에서 null을 빼고 전부 넣어줌
    4. 뒤에 암것도 없거나 뒤에 나오는놈이 nullable하면 지금까지 구한 지신의 FOLLOW랑 해당 생성규칙에서의 LHS의 FOLLOW랑 합집합 - 수식 적어가며 계산!
    5. 갱신이 안될때까지 4번 반복

Graph View

Backlinks