Fast Static Symbol Table, FSST (Encoding)

참고한 것들

• FSST: Fast Random Access String Compression, VLDB’20
• BtrBlocks - Efficient Columnar Compression for Data Lakes, SIGMOD’23

원본 논문

• 이 글은 FSST: Fast Random Access String Compression, VLDB’20 에서 핵심 아이디어만 요약한 글입니다.
• 별도의 명시가 없으면, 본 논문에서 그림을 가져왔습니다.

FSST §

• 이건 2020년 VLDB 에 소개된 string compression 방법이다.
• 방식은 “치환” 이라는 점에서 Dictionary Encoding 이랑 비슷한데, 좀 차이점이 있다. 더 자세한 내용은 아래에서 설명해 주마.
• FSST 의 특징은 이름이 시사하는 바처럼, (1) Symbol Table (2) Fast, (3) Static 이다.

특징 1) Symbol Table §

• 이 Symbol Table 은 한마디로 정리하면, Frequency-based substring substitution 이다. 이게 뭔뜻인지 알아보자.

Substring-substitution §

• Dictionary 가 개별 string domain 와 code 간의 mapping 이었다면,
• FSST 의 Symbol Table 은 최대 8byte (8 chars) 길이의, string domain 내의 substring (이것을 Symbol 이라고 부른다) 과 1byte code 간의 mapping 이다.
  • 위 그림 보면 쉽게 이해된다: http://in.tum.de 가 세 개의 Symbol (0:"http://", 6:"in.tum", 3:".de") 을 이용해 063 으로 표현되는 방식이다.
• 이 substring-substitution 방식은 실제 데이터를 관찰했을 때 비슷하지만 다른 문자열들이 많다는 결론에서 나온 것이다.
  • 이런 점에서 domain 전체에 대한 exact match 를 요하는 dictionary 에 비해 더 효율적으로 compression 이 가능하다.

Frequency-based §

• Symbol Table 의 code 는 1byte 이고, 따라서 모든 Symbol 이 담기는 것이 아니라 가장 빈도가 높은 255개만 담긴다.
• 근데 왜 256개가 아니고 255개일까? 이건 Escape 를 위해 code 하나 (255) 는 reserved 해놓았기 때문이다.
  • Symbol 의 개수가 255 개로 고정되어 있기 때문에, 분명히 어떤 놈은 이 Symbol 들로는 표현되지 않을 것이고, 그런 놈들을 처리하기 위해 Escape code 255 가 있는 것.
  • Escape code 뒤에는 문자 하나 (1byte) 가 오고, decompression 도중 이 Escape code 를 만나면 Symbol Table 에서 symbol 을 찾는 것이 아닌 바로 다음에 오는 이 문자를 result 에 넣는다.

특징 2) Fast §

• Symbol Table 을 보고 값을 치환하면 되기 때문에, decompression 과정이 아주 빠르다.
• 논문에는 이걸 더 빠르게 하기 위해 SIMD 와 같은 더 많은 최적화가 설명되어 있다. 궁금하면 직접 읽어보시라.

특징 3) Static §

• 이 Symbol Table 은 생성된 뒤에는, compression 및 decompression 과정에서 변경되지 않는다 (즉, Static 하다).
• 이건 Compressed data query 가 가능하다는 장점이 있다.
  • Block (string domain 의 sequence) 이 compressed 되어 있기 때문에, 여기에의 데이터를 가지고 꼼지락대고 싶다면 이것을 먼저 decompression 해야 하지만,
  • 개별적으로 Symbol table 을 이용해 치환하면 부분적으로도 decompression 이 가능하기 때문에, 전체를 decompression 하는 overhead 를 없앨 수 있다.
  • 혹은, 역으로 상대방을 compression 하는 방법도 사용할 수 있다.
    • 가령 WHERE 절의 = 연산자로 문자열 비교를 하는 상황이라고 해보자.
    • 그럼 compressed domain 을 decompression 하여 비교할 수 있지만,
    • 비교하고자 하는 uncompressed value 를 compression 하여 비교하는 것도 가능하다는 소리.
  • 이건 유일한 “상태” 인 Symbol Table 이 변경되지 않는다는 특징에 기반을 두고 있다. 하지만 LZ4 와 같은 애들은, compression 과 decompression 과정에서 이런 “상태” 가 바뀌기 때문에, 이런 compressed data query 를 사용할 수 없다.

Generating Symbol Table: Bottom-Up Symbol Table Construction §

요약 실패

• 짧고 깔끔하게 정리하고 넘어가려 했는데 요약이 잘 안되네요.
• 긴 글 참고 읽어봅시다.

논문 "Section 4. Symbol Table Construction"

• 논문에는 이러한 symbol table 생성 방법까지 오는 여정에 대해서도 설명되어 있다.
• Naive 하게 접근했을 때 발생하는 문제점인 Dependency problem 과 이를 해결하기 위한 첫번째 시행착오인 Suffix array 방식에 대해 더 알고 싶으면 논문을 참고하자.

• 그럼 딱 봐도 이 Symbol Table 을 어떻게 만드느냐에 따라 성능이 크게 좌우된다는 것을 알 수 있다. 그럼 이 문제의 Symbol Table 을 만드는 방법에 대해 알아보자.
• 우선 간략하게 설명하면, 아래의 과정을 총 5번 (5 Generation) 반복하며 symbol table 을 점진적으로 개선시키는 방식이다.
  1. 이전 Generation 에서의 symbol 들 중 어떤 symbol 을 하나 고른다.
  2. (1) 의 symbol 에 대해 입력 corpus 상에서 뒤에 연이어 나오는 또 다른 symbol 과의 조합 (즉, concat 이라고 이해하면 된다.) 을 알아낸다.
  3. (1) 과 (2) 의 두 symbol 로 compress 를 해보며 이 symbol 들이 몇번이나 사용되는지 count 한다.
  4. 또한 이 count 와 symbol length 를 곱한 Gain 을 계산한다.
  5. (1) ~ (4) 의 과정을 이전 Generation 에서의 모든 symbol 들에 대해 반복한다.
  6. 그럼 이전의 symbol 들, 그리고 이 symbol 들을 concat 한 새로운 symbol 들에 대한 Gain 들이 계산된다. 이들을 Gain 을 기준으로 정렬하고, 상위 255 개를 symbol table 에 추가한다.
  7. 다시 (1) 로 돌아가 새로운 Generation 을 시작한다.
• 그럼 이제 구체적으로 어떻게 하는지 Pseudo-code 로 알아보자.

Python style pseudo-code §

Member variables §

• 일단 FSST 에서는 두 가지 symbol 이 있다.
  • 첫째는 그냥 symbol. 그냥 흔히 생각할 수 있는 그 symbol 이다.
  • 두번째는 Pseudo-symbol 으로, 이건 위에서 말한 Escaped byte 를 위한 것이다.
    • 이 Escaped byte 를 위해 그냥 block 에 등장하는 문자만 symbol table 에 넣으면 저장공간을 줄일 수 있긴 하지만,
    • FSST 의 구현에는 block 에 실제로 등장하냐 와는 무관하게 ASCII 의 모든 문자 256 개를 전부 넣어놓고 시작한다.
    • 즉, 일종의 시간복잡도와 공간복잡도 사이에의 trade-off 간에 공간복잡도 보다는 시간복잡도를 절약하는 선택을 한 셈.
• 이때 각 member variable 들을 확인해 보자.

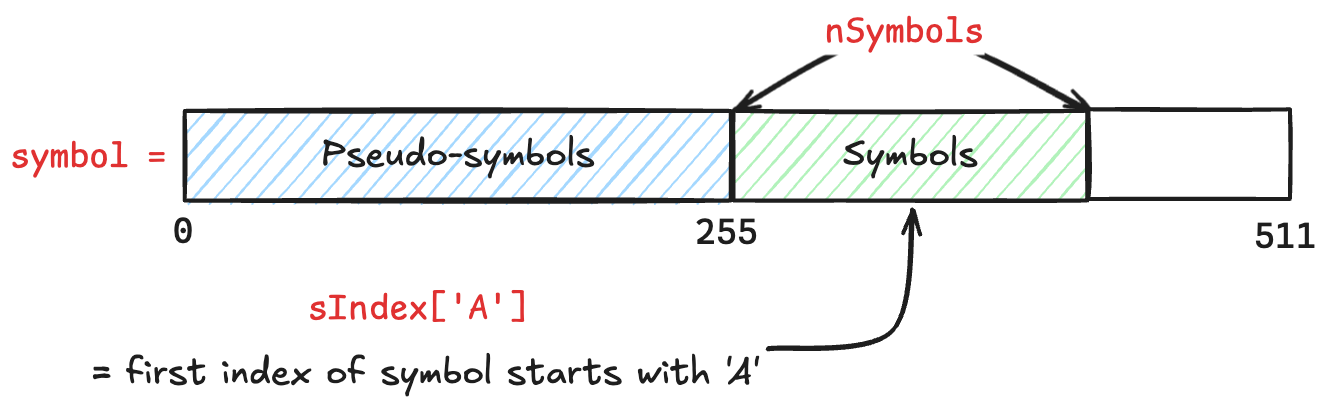
• nSymbols 는 그냥 symbol 의 개수를 나타낸다.
  • 따라서 처음에는 당연히 그냥 0 으로 초기화된다.
• symbols 는 모든 symbol 들을 모아놓은 배열이다.
  • 여기서 앞 256 개 에는 Pseudo-symbol 가 저장된다.
    • 즉, 여기에 해당 index 에 대응되는 ASCII 문자가 들어가 있는 것.
    • 여기서 볼 수 있듯이, escaped single byte 는 문자열에 등장하는 애들뿐만이 아닌 모든 문자들이 symbol 로서 등록되는 것을 알 수 있다.
  • 그리고 뒤의 256 개에는 진짜 symbol 이 저장된다.
    • 따라서 symbols 에 저장된 전체 symbol 의 개수는 $256+nSymbols$ 인 것.
    • 또한 256개의 symbol 은 (1) 알파벳 순서대로, (2) 길이가 긴 순서대로 정렬되어 있다.

Python chr() 함수

• 얘는 itoa 와 동일한 기능을 한다. 즉, 정수 -> ASCII 문자 변환인 것.

• sIndex 는 “어떤 문자” 로 시작하는 symbol 이 위치한 symbol array 의 시작 index 들을 저장하는 놈이다.
  • 이게 뭔소리냐면
  • 만약 'A' (ASCII: 65) 로 시작하는 symbol 이 symbol array 에서 어디에 있냐를 알고 싶으면
  • symbols[sIndex[65]] 를 참조하면 된다는 소리다.
  • 그리고 symbol array 에서 (Pseudo-symbol 들을 제외한) symbol 들은 정렬되어 있기 때문에,
  • symbol array 에서 sIndex[65] ~ sIndex[66] - 1 에는 모두 'A' 로 시작하는 symbol 들이 저장되게 된다.
  • 따라서 sIndex 는 sIndex(char) -> elementStartWithCharInSymbolArray 의 함수라고 이해해도 된다.

buildSymbolTable() §

• 이제 symbol table 을 생성하는 시작점인 buildSymbolTable 함수를 보자.
• 전체적으로 보면, 5번의 Generation 을 거치며 symbol table 이 보완되는 작업을 한다는 것을 알 수 있다.
• 여기서 첫번째 count1 배열은 해당 symbol 에 대한 빈도를 나타낸다.
  • 즉, count1(indexOfSymbolInSymbolArray) -> countOfTheSymbol 의 관계인 것.
  • 따라서 Pseudo-symbol 까지 해서 512크기가 되는 것.
• 그리고 두번째 count2 배열은 두 symbol 를 합쳤을 때의 빈도를 나타낸다.
  • 즉, count2(indexOfSymbolInSymbolArray, indexOfNextSymbolInSymbolArray) -> countOfCombinedSymbol 의 관계인 것.
• 이 두 count 들을 compressCount() 함수로 계산해낸 다음, 계산해낸 count 들을 이용해 makeTable() 로 symbol table 을 고쳐나가는 작업을 5번 반복하는 것이다.
• 그럼 이제 compressCount() 부터 어떤 짓을 하는지 볼텐데, 그 전에 이 함수에서 사용하는 helper 함수인 findLongestSymbol() 을 먼저 보고 가자.

findLongestSymbol() §

한줄 요약

• 인자로 받은 text 에 대한 Longest prefix symbol 을 찾아주는 것

• 우선 letter 에 text 의 시작문자에 대한 ASCII 정수가 담기고,
• sIndex 에서 이 letter 로 시작하는 symbol 들을 순회하며 알맞은 symbol 을 찾게 된다.
  • 위 에서 말한것 처럼, sIndex 는 어떤 문자에 대한 ASCII 정수값을 받아 해당 문자로 시작하는 symbol 들이 symbol array 에서 어디부터 있는지를 나타내기 때문에,
  • sIndex[letter] 부터 sIndex[letter + 1] 까지를 돌면 해당 letter 로 시작하는 모든 symbol 들을 다 반복문으로 돌릴 수 있다.
• 이때 이 loop 을 탈출하는 것은 prefix match 인것을 알 수 있다.
  • 위 에서 말한것 처럼, symbol 은 알파벳과 길이가 긴 순 으로 정렬되어 있기에,
  • 가장 먼저 매칭되는 symbol 이 곧 가장 길이가 긴 것이기 때문.
• 그리고 loop 을 다 도는 동안 매칭되는 symbol 이 없다면, escape 해야 한다는 소리이고, 그냥 letter 가 반환된다.
  • 여기서 letter 는 그냥 ASCII 정수이기 때문에 256 보다 작을 것이고, 따라서 findLongestSymbol 을 호출하는 놈은 리턴값이 256 보다 큰 값인지 아닌지로 symbol 인지 pseudo-symbol 인지 판단할 수 있다.

compressCount() §

한줄 요약

• 현재의 symbol 기준, 각 symbol 에 대한 count (count1) 와 두 symbol 의 조합에 대한 count (count2) 계산하기

• 좀 긴데, 차근차근 살펴보자.
• 일단 findLongestSymbol() 로 pos 가 가리키는 지점에서부터의 longest prefix symbol 을 찾아 code 에 넣는다.
• 그리고 해당 symbol 의 길이만큼 pos 를 옮겨준 뒤, code 를 prev 에 복사해 넣고, 또 한번 findLongestSymbol() 을 돌려 다음 code 를 찾는다.
• 이후 뭔 짓을 한 뒤, 다음 loop 에서 code symbol 길이만큼 pos 를 옮겨주고, prev 를 code 로 설정해 준 뒤, code 를 새로 구해준다.
• 따라서 각 loop 에서 pos, prev, code 가 다음과 같이 유지된다는 것을 알 수 있다.

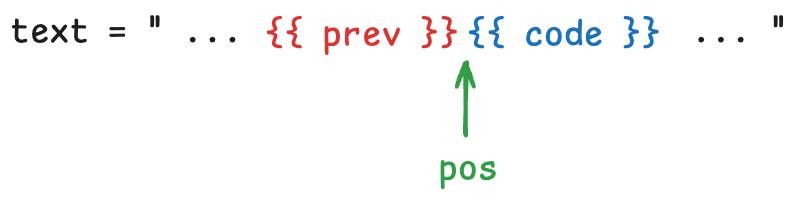
• 이때, 매 loop 에서 count1 와 count2 를 계산해 준다.
  • code 하나에 대한 count 를 1 증가시켜준다. 당연히 하나의 symbol 에 대한 count 이므로 count1 을 업데이트한다.
  • prev 와 code 에 대한 count 를 1 증가시킨다. 연이은 symbol 조합에 대한 count 이므로 count2 를 업데이트한다.
  • 그리고, code 가 256 보다 크다면, 이놈이 Pseudo-symbol 이 아니라는 의미이다. 따라서, prev 뒤이어 나오는 code 뿐 아니라 Pseudo-symbol 에 대한 조합도 count 를 증가시킨다.
    • 이것은 prev 와 code 모두 longest symbol 정책으로 선택되기에, 이 방식으로는 중간 크기의 symbol 에 대해서는 반영되지 않는 문제점을 보완하기 위한 것이다.
    • 즉, prev 뒤에 Single byte extension 을 조합한 symbol 또한 반영하여 longest 만을 고집하여 발생하는 문제점을 없애주기 위함이다.

makeTable() §

한줄 요약

• Symbol 들에 대한 Gain 을 계산하고 정렬해 상위 255개를 symbol table 에 추가한다.

• 크게 세 부분으로 나뉜다.

1. compressCount() 로 구한 count 를 이용해 Gain 을 구하고, 이것으로 정렬된 cand array 만들기
   • 일단 code1 에 대한 loop 에서는, Pseudo-symbol (0 ~ 255) 과 그냥 symbol (256 ~ 256 + nSymbols) 까지 쭉 돌며 Gain 을 계산하고, heap 을 이용해 정렬하며 cand 에 넣는다.
   • 그리고 code2 에 대한 중첩 loop 에서는, 마찬가지로 Pseudo-symbol 과 그냥 symbol 을 쭉 돌며 code1 + code2 의 concat 에 대한 Gain 을 계산하고 정렬하여 cand 에 넣는다.
2. cand array 로부터 255 개를 꺼내어 symbol table 구성하기
   • cand 가 Gain 으로 정렬되어 있기 때문에 이 중 상위 255개를 골라 symbol table 에 넣는다.
3. sIndex 새로고침하기
   • cand 는 Gain 을 기준으로 정렬되어 있었는데, symbol table 은 위 에서 설명한 것처럼 알파벳 순서대로 정렬되어 있다.
   • 따라서 symbol table 의 symbol 들을 새로 정렬하며 sIndex 의 원소들이 올바른 위치를 가리키도록 새로고침해줄 필요가 있다.
   • 이건 다음 섹션 에서 설명할 makeIndex() 함수에서 수행한다.

makeIndex() §

한줄 요약

• Gain 기준으로 정렬되어 있던 것을 알파벳순 (Lexicographical order) 로 재정렬하며 sIndex 값을 업데이트한다.

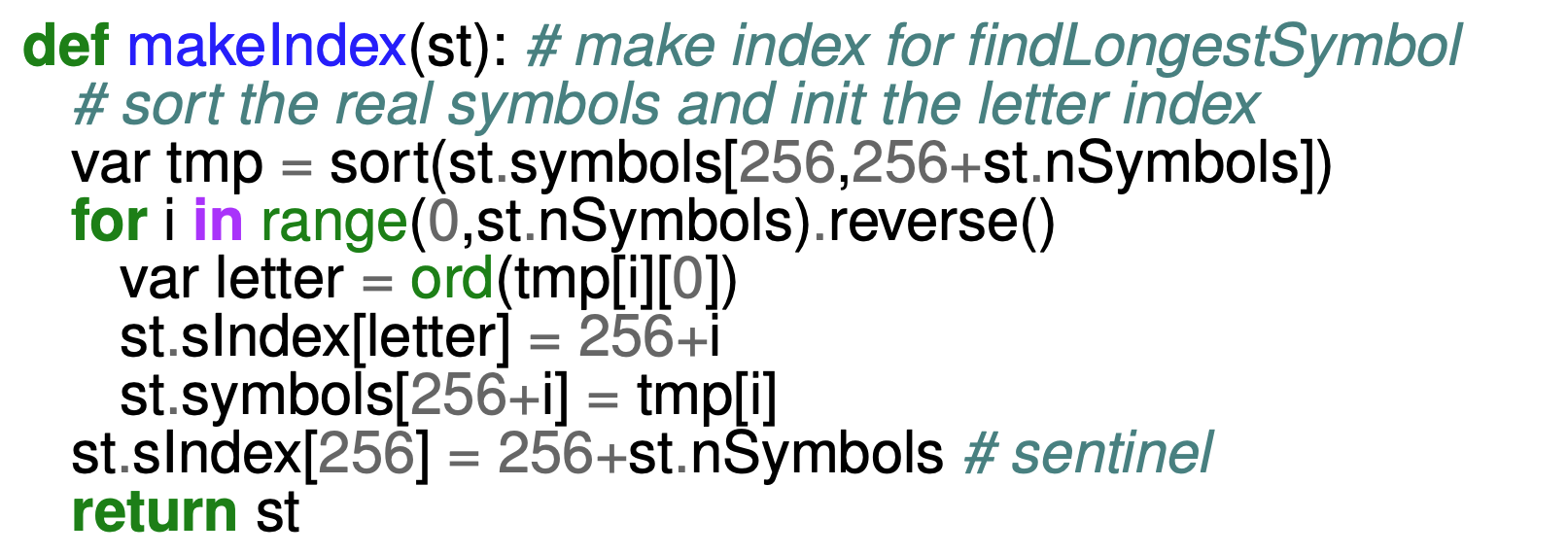
• 우선 sort() 으로 symbol 구간 (256 ~ 256 + nSymbols) 을 알파벳순으로 정렬한 tmp 를 하나 준비한다.
• 그리고 loop 을 돌며 sIndex 를 업데이트하는데,
  • 일단 한번의 loop 에서는 다음과 같이 업데이트한다:
    • tmp 의 $i$ 번째 원소의 첫번째 문자 letter 에 대해
    • sIndex 의 letter index 값을 $256+i$ 로 업데이트한다.
    • 그리고 symbol array 에서의 이 $256+i$ 인덱스에 해당하는 값이 $i$ 번째 원소가 되게 한다.
    • 이렇게 함으로써, 어떤 ‘문자’ 를 symbol array 에서의 index 로 변환하는 sIndex 값이 업데이트된다.
  • 근데 여기서 고려할 점은 tmp 의 역방향으로 loop 을 돈다는 점이다. 즉, $i$ 값은 loop 가 돌며 감소하는 값이다.
    • 이렇게 함으로써 정렬된 tmp 내에서 어떤 ‘문자’ 로 시작하는 symbol 들의 첫 index 가 sIndex 에 저장될 수 있게 한다.
    • 가령 tmp = [abc, acd, ad] 였다고 해보자.
    • 그럼 ad -> acd -> abc 순서로 loop 를 돌면, 결국에는 'a' 로 시작하는 제일 첫 symbol 인 abc 가 마지막에 덮어씌워지며 sIndex 에는 abc 에 대한 index 가 저장되는 것이다.

#draft 예시

• 논문에 예시가 있긴 한데, 위의 Pseudo-code 와는 좀 다르다. 따라서 일단 생략하고 나중에 정리하자..