참고한 것들
“차이”
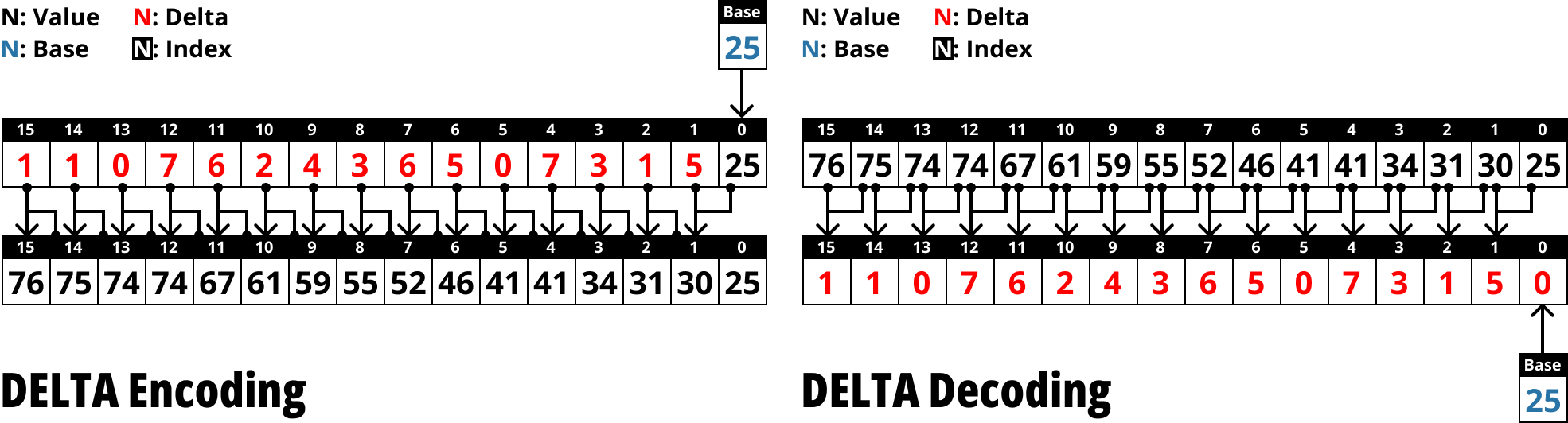
- 개념은 쉽다. 어떤 값을 그대로 저장하기보다는, 앞선 값과의 “차이 (Delta)” 를 저장하는 방식이다.
- 이것을 조금 유식하게 (그리고 짜증나게) 표현해 보면,
- 이전 값이 다음에도 동일할 것이라고 예측 했을 때, 이 예측 값과 관찰 값의 차이를 저장하는 방식이라고 생각해서 Predictive scheme 이라고 부르기도 한다.
- 이에 따라 이 이전값을 Prediction 이라고 하는 경우도 있다.
- FOR 와 이것의 공통점은, 둘 다 어떤 큰 값을 작은 값으로 변환하는 방식이라는 점이고, 따라서 보통 encoding 이후에 BP 로 bit 수를 줄여주게 된다.
- 예시로 보자면, 다음의 배열은
[107,108,110,115,120,125,131,132,132,135]
- 이렇게 바뀌고
initial=107
[1,2,5,5,5,6,1,0,3]
- 여기에 BP 까지 적용하면 의 데이터가 으로 줄어들게 된다.
음수 처리
- 근데 여기에는 문제가 있다.
- 위와 같이 모든 값들이 깔끔하게 0 이상의 정수로 나온 것은 이놈이 정렬 되어 있기 때문이다.
- 물론 값들이 순서가 상관 없으면 정렬해서 delta encoding 을 하면 되긴 하지만, 항상 순서가 무관하리라는 보장은 없기 때문에 delta 가 음수 가 되는 경우를 처리해 줘야 한다.
- 이 음수를 처리하는 방법은 3가지 정도 있다. 이것을 아래의 예시로 알아보자.
original: [107,108,110,115,120,125,132,132,131,135]
delta: [1,2,5,5,5,7,0,-1,4]
Modulo (Unsigned)
- 원래의 값 (
original) 이 8bit 이기에 이것으로 설명하면, - 이므로 이라고 할 수 있다.
- 즉, 어찌 보면 그냥 원래 음수를 표현하던 방식인 2의 보수 를 활용하는 것.
- 따라서 signed int 를 unsigned int 로 해석하면 된다. 다음의 C++ 예시를 참고하시라.
#include <iostream>
#include <vector>
template<typename T>
void print(std::vector<T> vec) {
auto back = vec.back();
vec.pop_back();
std::cout << "{";
for (auto el : vec) {
std::cout << (int)el << ", ";
}
std::cout << (int)back << "}" << std::endl;
}
int main() {
std::vector<int> delta = {1,2,5,5,5,7,0,-1,4};
print<int>(delta);
std::vector<u_int8_t> enc;
for (auto d : delta) {
enc.push_back(d);
}
print<u_int8_t>(enc);
std::vector<int8_t> dec;
for (auto e : enc) {
dec.push_back(e);
}
print(dec);
}{1, 2, 5, 5, 5, 7, 0, -1, 4}
{1, 2, 5, 5, 5, 7, 0, 255, 4}
{1, 2, 5, 5, 5, 7, 0, -1, 4}
참고: C++
u_int8_t
- 코드에서는
u_int8_t로 적었지만, 사실 이건char와 같다. 따라서print()함수에서(int)로 형변환을 해주고 있는 것.
Zig-zag encoding
- Zig-zag Encoding 을 사용하면 음수를 양수로 만들 수 있기 때문에, delta 가 음수가 되는 것을 이것으로 양수로 만들 수도 있다.
XOR
- 마지막 방법은 delta (뺄셈 연산) 말고 XOR 를 사용하는 것이다.
- 양수는 most significant bit 가 항상 0이므로, 양수끼리의 XOR 는 절대로 음수를 생성하지 않는다.
- 물론 음수와 양수를 XOR 를 하면 음수가 나오긴 하는데, 이때는 위의 Modulo 와 같이 처리해야 할듯.
- 다음의 예시를 보자.
#include <iostream>
#include <vector>
void print(std::vector<int> vec) {
auto back = vec.back();
vec.pop_back();
std::cout << "{";
for (auto el : vec) {
std::cout << el << ", ";
}
std::cout << back << "}" << std::endl;
}
int main() {
std::vector<int> target = {107,108,110,115,120,125,131,132,132,135};
print(target);
std::vector<int> enc;
for (auto it = target.begin(); it < target.end() - 1; it++) {
enc.push_back(*it ^ *(it + 1));
}
print(enc);
}{107, 108, 110, 115, 120, 125, 131, 132, 132, 135}
{7, 2, 29, 11, 5, 254, 7, 0, 3}
하지만 BP 가 안되는데요?
- 보면 Zig-zag 의 경우는 그렇다 쳐도, Modulo 랑 XOR 의 경우에는 중간에
255나254같은 야리꾸리한 값들이 있다는 것을 알 수 있다. - 따라서 이런 요사스러운 애들에 대해서는 Patching 을 이용하여 BP 를 하게 된다.
언제 쓰면 좋을까?
- FOR 를 쓸 수 있는 상황이면 Delta 도 좋다; 값들의 range 가 작을 때 사용하면 좋다.
- 하지만 FOR 와의 차이점은, Delta 의 경우 범위가 넓어도 두 값의 차이가 작으면 사용할 수 있다.
- 대표적으로 SQL 의
SEQUENCE를 생각해 보자. 얘는 꾸준히 1씩 증가하므로 전체적으로는 범위가 진자루 넓지만, 각 값들 간의 차이는 1밖에 안나기 때문에 Delta 를 적용하면 1로 통일되게 된다.
- 대표적으로 SQL 의