02. Binary Representation

서울대학교 컴퓨터공학과 이재진 교수님의 "확장형 고성능 컴퓨팅" 강의를 필기한 내용입니다.

• 목차

Numeric system §

• “수” 는 추상적인 개념, “숫자” 는 “수” 를 표현하는 표현법 (representation)
• Positional number system: 숫자의 위치에 따라 weight 가 달라지는 것
  • 일반적으로 알고있는 숫자 시스템이 이거다: 가령 십진수 365 에서 3은 $10^2$ 의 weight, 6은 $10^1$ 의 weight 인 것 처럼

Signed, Unsigned §

• Unsigned: 0 이상 정수. 얘를 표현하는 것은 별 문제가 없다.
• Signed: 모든 정수. 얘를 표현하는게 문제다.

Sign-magnitude §

• 가장 단순한 생각은 MSB 로 부호를 표현하고, 나머지로 숫자를 표현하면 된다는 것이다.
• 이것을 Sign-magnitude 라고 하고, 이 방식의 문제점은 대략:
  • 더 많은 register 사용하게 된다는 것과
  • 양의 0 과 음의 0 이 존재한다는 점 (0000... 와 1000...) 이 있다.

Radix Complements §

• 주객전도식으로 설명하자면, Radix complement 는 2 (혹은 1) 의 보수에 대한 N-진법 대상 일반화이다.
• 일단 base $r$ 에 대해 ”$r$ 의 보수” 는 $f_r(x)=r^n-x$ (단, $x=0$ 이면 $f(x)=0$) 로 정의한다.
• 그리고 ”$r-1$ 의 보수” 는 $f_{r-1}(x)=r^n-1-x$ 로 정의한다.
  • 참고로 저 $r-1$ 에서 $-1$ 은 뺄셈이 아니다.
  • 그냥 ”$r-1$ 의 보수” 가 맞는 표현이고, 저것을 뺄셈으로 취급해 계산해서 호칭하는 것은 잘못된 것이라는 것.
  • 한마디로 ”$1$ 의 보수” 가 아니라 ”$2-1$ 의 보수” 가 맞는 표현이라는 소리다.
  • 물론 근데 귀찮아서 주인장도 ”$1$ 의 보수” 라고 말할 예정.
• 따라서 $f_r(x)=f_{r-1}(x)+1$ 이다.

$r$ vs $r-1$ complement §

• Signed integer 에서 음수를 bit 으로 표현할 때 1의 보수 ($r-1$’s complement) 를 사용하는 것은 여전히 양, 음의 0 이 있는 문제가 있다.
  • 0000... 은 양의 0, 1111... 은 음의 0
• 그래서 거의 모든 architecture 에서는 2의 보수 ($r$’s complement) 를 사용한다.
  • 여기에서는 이런 문제가 없고,
  • 연산하는 것도 bit reverse 하여 1의 보수로 만든 다음 1을 더해주면 되기 때문에 아주 편하다
  • 심지어 뺄셈도 그냥 2의 보수로 만든 다음 덧셈회로에 찔러주면 된다.
• 참고로 1의 보수 표현에서의 범위는 $-2^{n-1}+1\le N\le 2^{n-1}-1$ 이고, 2의 보수 표현에서는 $-2^{n-1}\le N\le 2^{n-1}-1$ 이다.

Operation §

• 음수의 나눗셈에 대해서는 Euclidean division 을 사용한다.
  • 즉, 나머지는 무조건 양수인 것.
  • 가령 $-7÷3$ 는 $3\times -3+2$ 가 되어 몫이 $-3$, 나머지는 $2$ 이다.
• 모든 연산에 대해서는 연산 이후 mod 를 씌워서 overflow 를 절삭한다.
  • 이와 같은 연산법을 Modulo-m operation 라고 한다.
  • 이에 따라 mod 가 같으면 같은 값이 된다 (Congruence relation).
  • 가령 3-bit 에서 5 와 13 은 같고 ($13\mathrm{mod}8=5\mathrm{mod}8=5$),
  • 7+3 의 결과는 2 다 ($(7+3)\mathrm{mod}8=2$).

Bitwise §

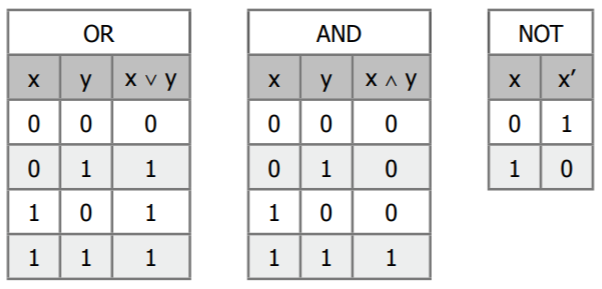
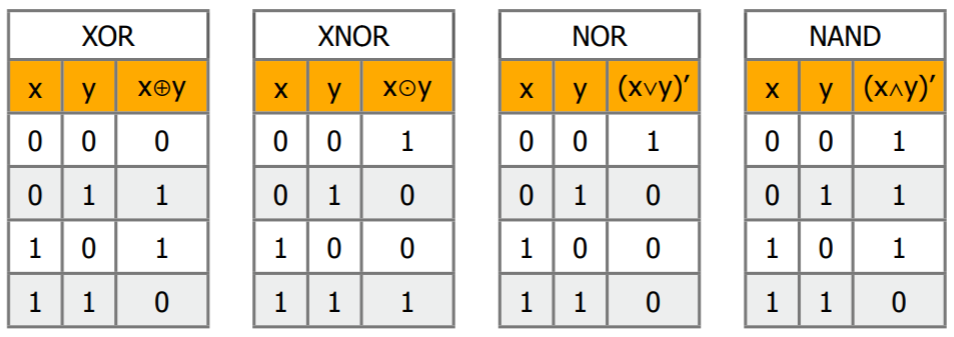
• 뭐 이건 계산방법만 위 그림 보고 익혀두면 된다.
  • XOR: 다르면 1
  • XNOR: 같으면 1
  • NOR: not-OR
  • NAND: not-AND
• 참고로 NAND (과 NOR) Functionally complete 하다고 한다.
  • 즉, NAND 만 가지고 (혹은 NOR 만 가지고) AND, OR 등의 모든 bitwise 를 표현할 수 있다.

Logic Gate §

• Logic gate 는 위와 같은 bitwise 에 대한 (논리적 혹은 물리적) 구현체라고 생각하면 된다.
  • 즉, 이놈은 하나 이상의 bitwise operation 을 수행하는 unit 인 것.
• 조금 수학적으로 표현해 보자면,
  • $B$ 가 집합 $\{0,1\}$ 이고
  • $B^n$ 는 길이 $n$ 의 binary stream 일 때,
  • Logic gate 는 $f:B^n\to B^m$ 의 함수이다.
• 보통은 이것을 그림 (기호) 으로 abstract 한다.
  • 아래 그림 참고하시게

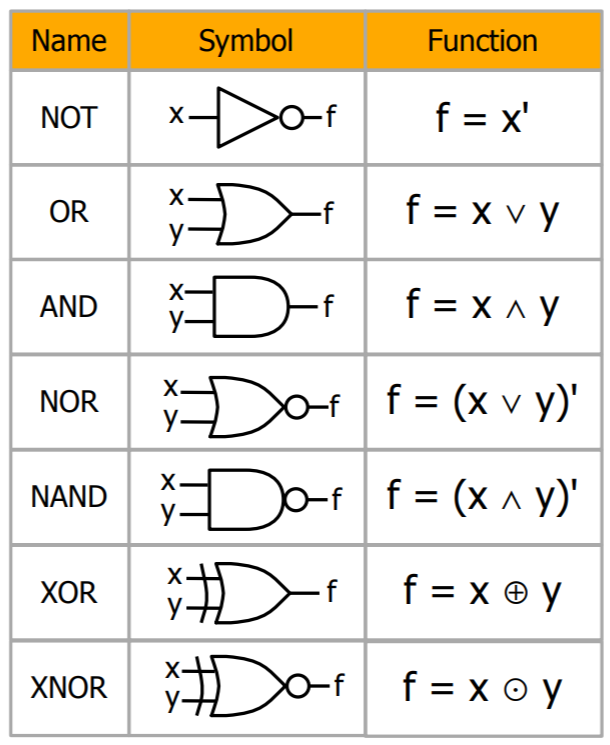
• 어떤 한 logic gate 를 다른 logic gate 들로 나타내는 것을 Combination 이라고 한다.
  • 가령 아래 그림은 XOR 를 AND, OR, 그리고 NOT 으로 나타낸 것이다.

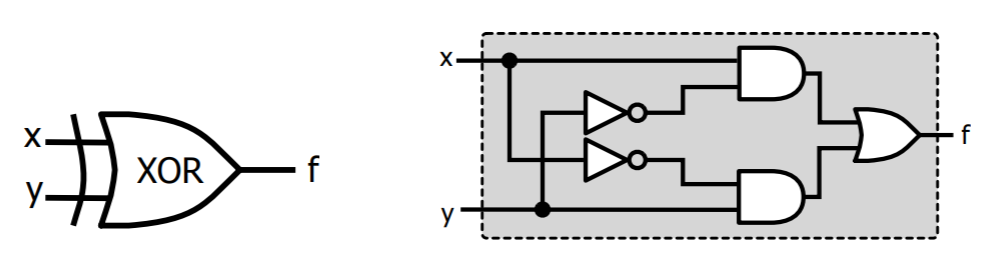
Shift §

• Shift 에는 두 종류가 있다:
  • Logical shift 는 너가 생각하는 그거다: Shift 하면서 생긴 빵꾸에는 무조건 전부 0을 채운다.
  • Arithmetic shift 는 right shift 가 다르다: Right shift 할 때의 빵꾸는 MSB 로 채운다.
    • 즉, 음수면 음수가 유지된다는 것.
• 당연히 lshift 는 곱셈, rshift 는 나눗셈에 대응
  • 따라서 arithmetic rshift 를 하면 euclidian division 의 몫이 나온다.
• C 에서는 compiler 마다 다를 수 있다.
  • 이건 C99 표준에는 이것에 대해 정의하고 있지 않 기 때문.
  • GCC 의 경우에는 signed integer 의 경우에는 arithmetic shift 를 해서 부호를 유지하고, unsigned integer 의 경우에는 logical shift 를 해서 양수를 유지한다.

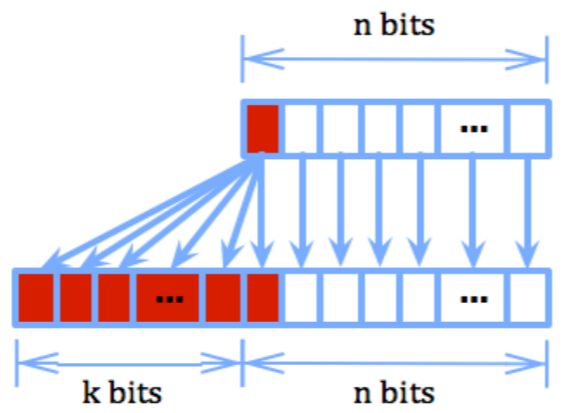
Sign extension §

• Sign extension 은 BP unpack 시에 빈공간들을 뭐로 채우냐에 대한 내용이다.
• 당연히 packed bit 는 그대로 가져오고 넓어진 공간은 packed bit 의 MSB 로 채운다.

Addition Overflow §

Unsigned int §

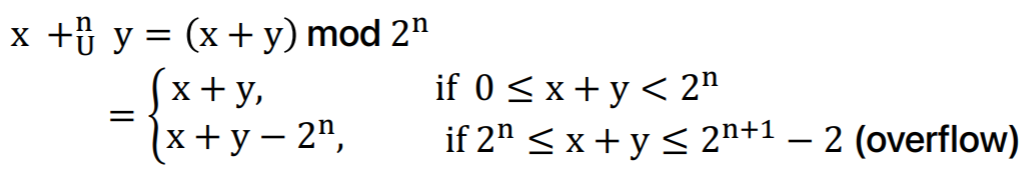
• $X+Y=(X+Y)\mathrm{mod}{2}^n$ 이므로 $[0,2^n-1]$ 에 들어온다.
• 근데 수치적으로 $X$ 와 $Y$ 는 각각 $[0,2^n-1]$ 이므로 $X+Y$ 는 $[0,2^{n+1}-2]$ 까지다.
• 따라서 $X+Y$ 에서 $[2^n,2^{n+1}-2]$ 는 mod 에 의해 절삭된 overflow 이다.

Signed int §

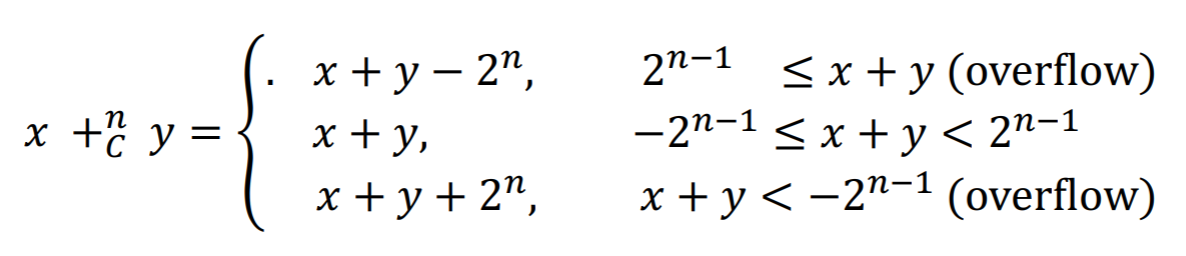
• $X$, $Y$ 모두 양수인 경우에는 $[2^{n-1},2^n-2]$ 가 overflow 이다.
  • 각각은 $[0,2^{n-1}-1]$ 에 들어오기 때문에 더하면 $[0,2^n-2]$ 인데 $X+Y$ 는 $[0,2^{n-1}-1]$ 에 들어와야 하기 때문.
  • 이 경우에 대해서는 MSB 가 0에서 1로 바뀌기 때문에 2’s complement 의 관점에서는 양수의 덧셈이 음수가 되는 것처럼 보인다.
• $X$, $Y$ 모두 음수인 경우에는 $[-2^n,-2^{n-1}+1]$ 가 overflow 이다.
  • 각각은 $[-2^{n-1},0]$ 에 들어오기 때문에 더하면 $[-2^n,0]$ 인데 $X+Y$ 는 $[-2^{n-1},0]$ 에 들어와야 하기 때문.
  • 이 경우에는 반대로 MSB 가 1에서 0으로 바뀌고, 따라서 음수의 덧셈이 양수가 되는 것 처럼 보인다.
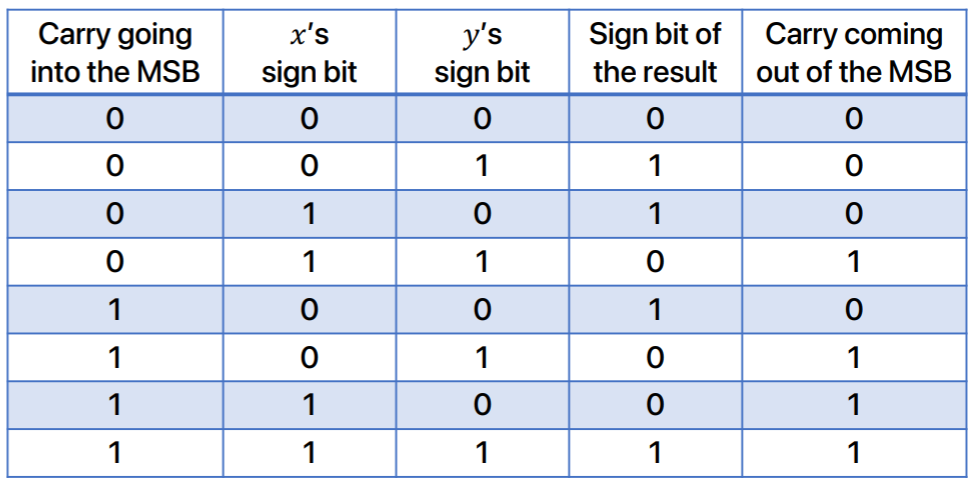
• 이것을 다르게 정리하면, MSB 의 계산에 사용되는 carry bit (carry going into the MSB) 와 MSB 계산 후의 carry bit (carry coming out of the MSB) 가 다르다면, overflow 가 난다.
  • 아래의 표를 보시라; 외울건 아니고 생각해보면 당연한 것이긴 하다.
  • 근데 이것이 중요한 이유는 다음에 나오는 adder 때문이다.
  • 즉, 두 carry bit 가 다르면 overflow 이기 때문에, 두개를 XOR 하여 overflow 를 감지할 수 있기 때문.

Adder §

Half, full bit adder §

• Half adder: 비트 두개 ($x$, $y$) 를 받아 결과 ($s$) 와 carry bit ($c^{out}$) 를 반환
• Full adder: 비트 두개 ($x$, $y$) 와 carry input ($c^{in}$) 을 받아 결과 ($s$) 와 carry out ($c^{out}$) 을 반환
  • 뭐 대략 아래처럼 생겼댄다. 외우지는 않아도 됨

N-bit unsigned int adder §

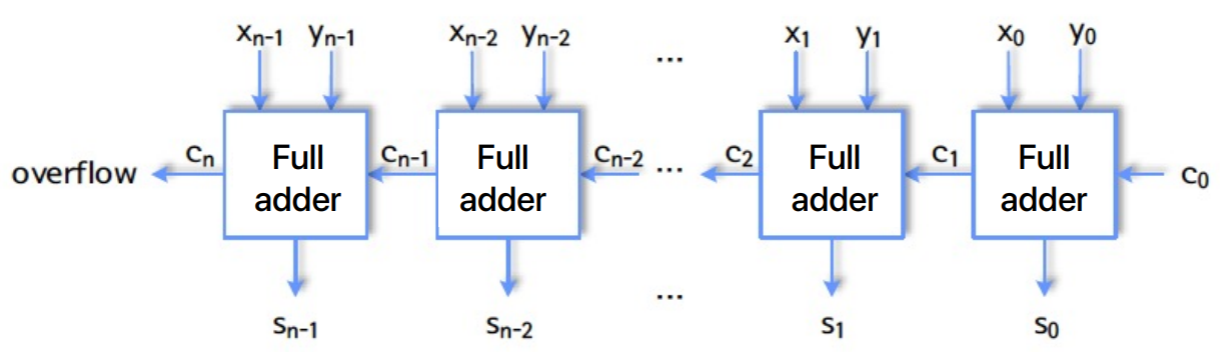
• 따라서 Half adder 하나와 Full adder $N-1$ 개를 이어붙이면 $N$-bit unsigned int adder 가 된다.
  • 즉, $Ad{d}^u:X\{x_0,...,x_{n-1}\},Y\{y_0,...,y_{n-1}\}\to S\{s_0,...,s_{n-1}\},c_n^{out}$
  • 이때는 마지막 carry ($c_n^{out}$) 이 1이면 overflow 이다.
  • 위 그림에는 모두 full adder 인데 상관없다.

N-bit signed int adder §

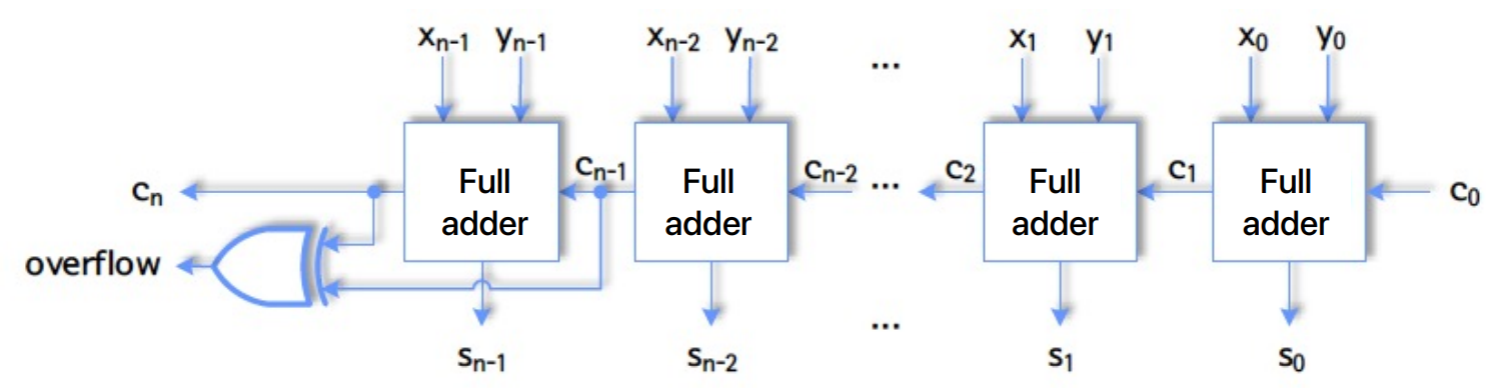
• 그리고 그냥 Full adder 를 $N$ 개 이어붙이면 $N$-bit signed int (2’s complement) adder 가 된다.
  • 즉, $Ad{d}^s:X\{x_0,...,x_{n-1}\},Y\{y_0,...,y_{n-1}\},c_0^{in}\to S\{s_0,...,s_{n-1}\},c_n^{out}$
  • 이때는 위에서 말한 MSB 양쪽의 carry bit 가 같은지 다른지를 통해서 overflow 알아낸다.
  • 즉, $XOR(c_{n-1}^{out},c_n^{out})$ 으로 알아낼 수 있고, 이것을 그림으로 그려보면 아래와 같다.

Subtractor §

Half, full bit subtractor §

• Adder 가 carry bit 를 필요로 했다면, Subtractor 는 borrow bit 를 필요로 한다.
  • 즉, 0 - 1 의 경우 1 를 앞에서 빌려와야 하기 때문.
• 따라서 half, full 도 adder 에서의 carry 를 그냥 borrow 로 바꾸면 됨
  • Half subtractor: 이놈은 bit 두개 ($x$, $y$) 를 받아 결과 ($d$) 와 borrow bit ($b$) 를 반환한다.
  • Full subtractor: 이놈은 bit 두개 ($x$, $y$) 와 borrow in ($b^{in}$) 를 받아 결과 $d$ 와 borrow out ($b^{out}$) 을 반환한다.
    • 여기서 borrow in 은 앞선 연산이 빌려간 것, borrow out 은 현재 연산이 빌리는 것이라고 생각하면 된다.
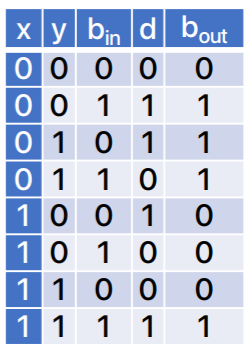
    • 이놈의 경우 어떻게 연산되는지 헷갈릴 수 있는데, 다음의 표를 참고하자.
    • 다만 저 $x=0$, $y=1$, $c^{in}=1$ 일 때 $d=0$, $c^{out}=1$ 이 되는 상황이 잘 이해가 안된다면, 1 bit 를 빌려와 $x=2$ 가 되고, 여기서 $y$ 와 $c^{in}$ 이 하나씩 빼가니까 결과는 0이고, 1을 빌려온 것이 된다.

N-bit unsigned subtractor §

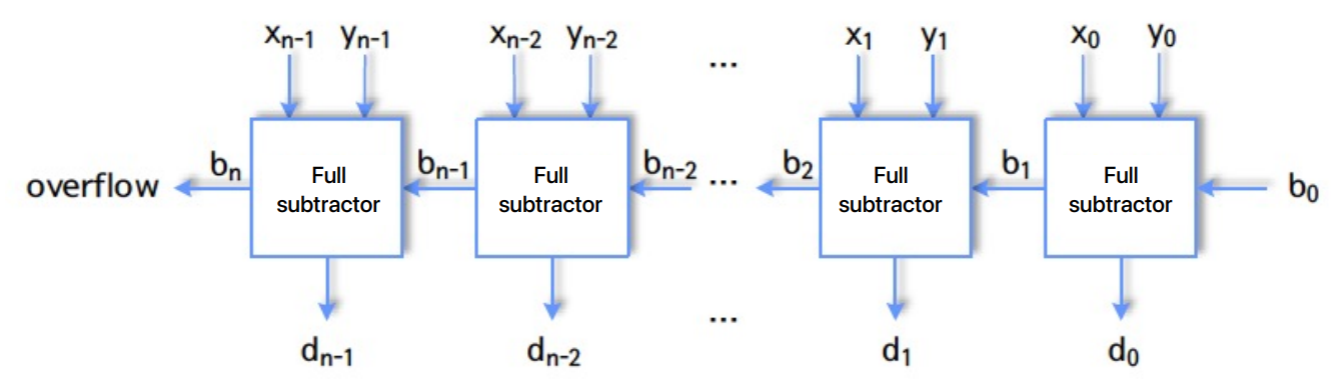
• $N$-bit unsigned subtractor 는 그냥 half subtractor 하나와 full subtractor $N-1$ 개를 이어붙이면 된다.
  • 즉, $Su{b}^u:X\{x_0,...,x_{n-1}\},Y\{y_0,...,y_{n-1}\}\to D\{d_0,...,d_{n-1}\},b_n^{out}$
  • 뭐 위 그림에는 모두 full subtractor 이긴 한데 이 차이는 별 의미 없다

N-bit signed subtractor §

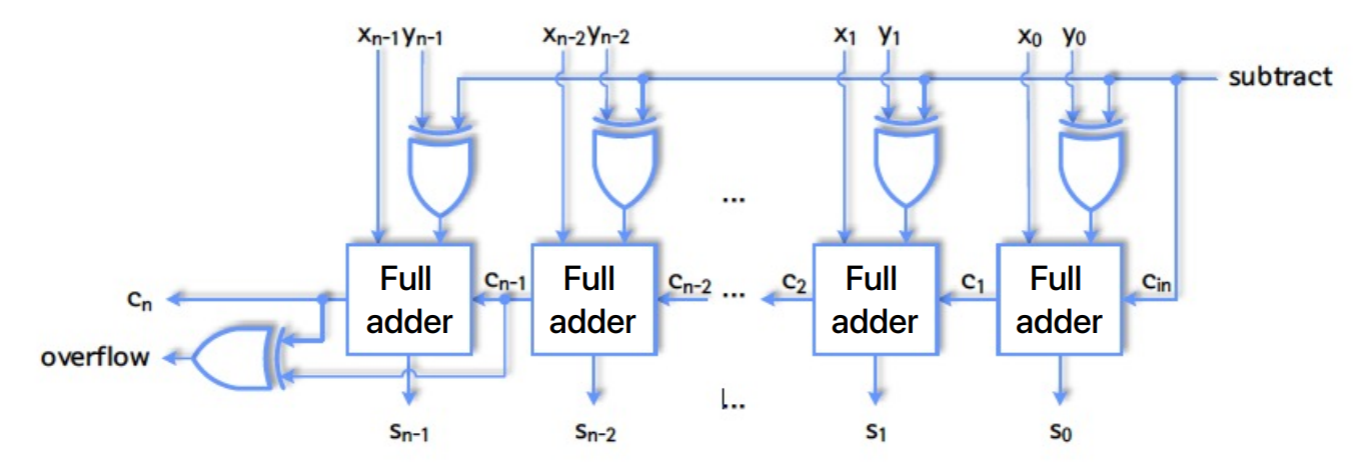
• 여기서의 아이디어는 그냥 하나를 2의 보수로 음수로 만든 다음 N-bit signed adder 를 사용하자는 것이다.
  • 2 의 보수로 만드는 것은 bit 를 다 뒤집어야 하기 때문에, subtract bit 을 하나 받아서 $Y$ 의 모든 bit ($\{y_0,...,y_{n-1}\}$) 에 XOR 을 해주고
  • 또한 1을 더해줘야 하기 때문에, 이 1 은 $c_0^{in}$ 에다 집어넣는다.
• 즉, 위 그림처럼 되는 것.

Multiplier, Divider §

부실한 설명

• 설명이 좀 부실하긴 한데, 자세하게는 몰라도 되니까 패스

• 곱셈은 10진수 곱셈 생각하면 된다.
  • 각 자릿수를 곱해주고 더해주는 것을 반복하듯이
  • 각 bit 를 AND 해주고 더해주는 것을 반복한다.
  • 즉, AND gate 와 N-bit signed bit adder 를 여러개 사용해서 구현한다.
• 곱셈/나눗셈:
  • 나눗셈은 뺄셈의 연속이므로 substractor 를 여러개 가져와서 사용
• 참고: MUX (muliplexer): 입력 X, Y 와 selector 총 세개의 입력을 받아 selector 에 따라 X 혹은 Y 를 결과로 반환