Madison Digital Garden

Search

SearchSearch

05. Data Level Parallelism (Advanced Computer Architectures, SNU CSE)

Mar 18, 2025, 12 min read

서울대학교 컴퓨터공학부 유승주 교수님의 "고급 컴퓨터 구조" 강의를 필기한 내용입니다.

SIMD

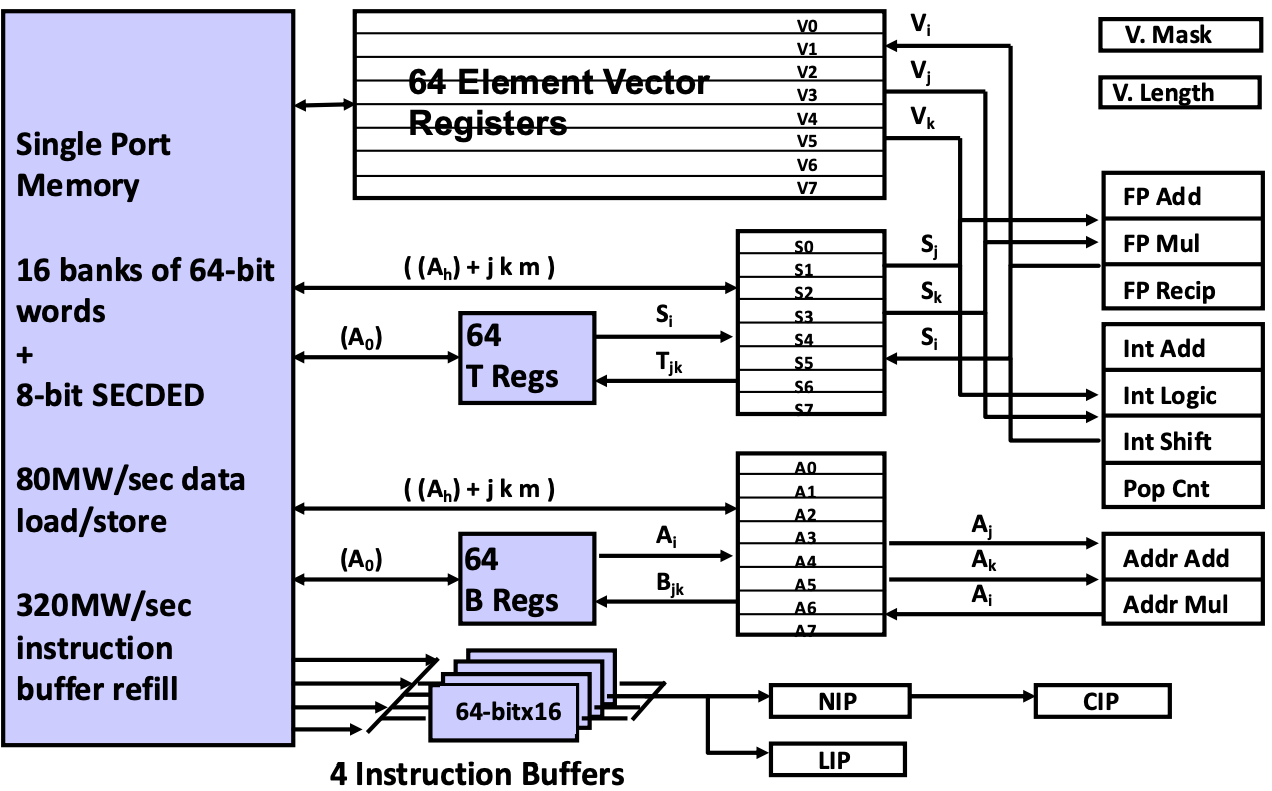
  • SIMD 에서는 레지스터의 크기가 애초에 커서 여기에 여러개의 word 를 담고, 이것을 여러개의 ALU 에 한번에 던져서 parallel 하게 처리한다.

  • 위 그림이 SIMD 를 제공하는 아주 고전적인 architecture 인 Cray-1 인데,
    • 다 볼 필요는 없고 저기서 위쪽의 vector register 만 보면 된다.
    • 보면 64-element vector registers 라고 되어 있는데, 이 말이 하나의 register 에는 64개의 element word 가 vector 로써 들어가고
    • 따라서 register 에 있는 데이터가 오른쪽의 ALU 에 들어가게 되는 거다.
      • 다만 ALU 에서 한번에 처리하는 개수는 이것보다는 더 작을 수도 있다.

Vector, SIMD

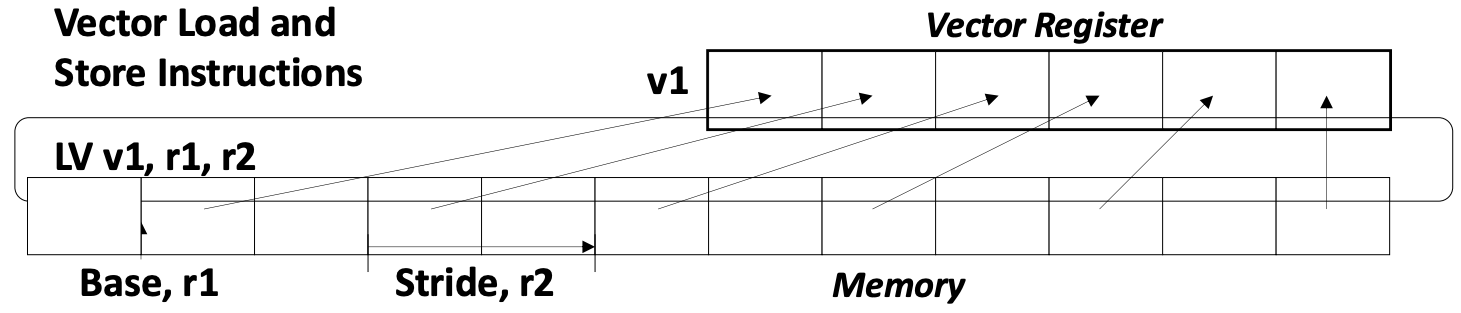
  • Vector 랑 SIMD 는 조금의 차이점이 있지만 거의 비슷한 용어이다.
    • Vector processor 에서는 위 그림에서 보여지는 것 처럼 연속되지 않은 DRAM 공간의 데이터도 load 할 수 있다는 차이점이 있는데
      • 이건 것을 stride access pattern 이라고 한다.
    • 근데 SIMD 도 요즘 이런게 가능해서 거의 차이가 없는 용어라고 한다.

Vector Pipelining

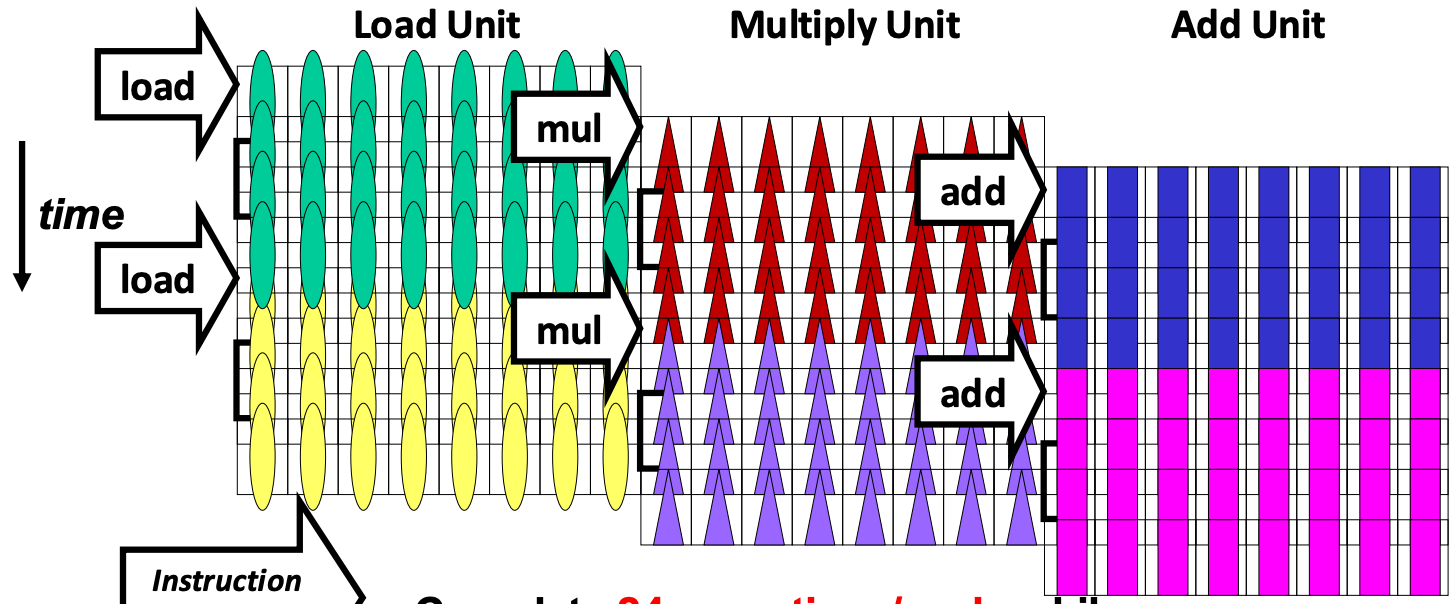
  • Vector 에서도 Pipeline 이 가능하다.
    • 위 그림은 48개의 element 가 들어가는 register 에 대해 8-lane (즉, 한번에 연산하는 element 의 수) 으로 pipeline 을 하는 것인데,
    • 보면 8개를 먼저 load 하고, 그 다음 8개를 load 하는 동안 8개를 multiply 하는 방식으로 pipeline 되는 것.

Matrix Multiplication Example w/ SIMD

  • SIMD 를 이용해 행렬곱을 하는 예시를 한번 보자.

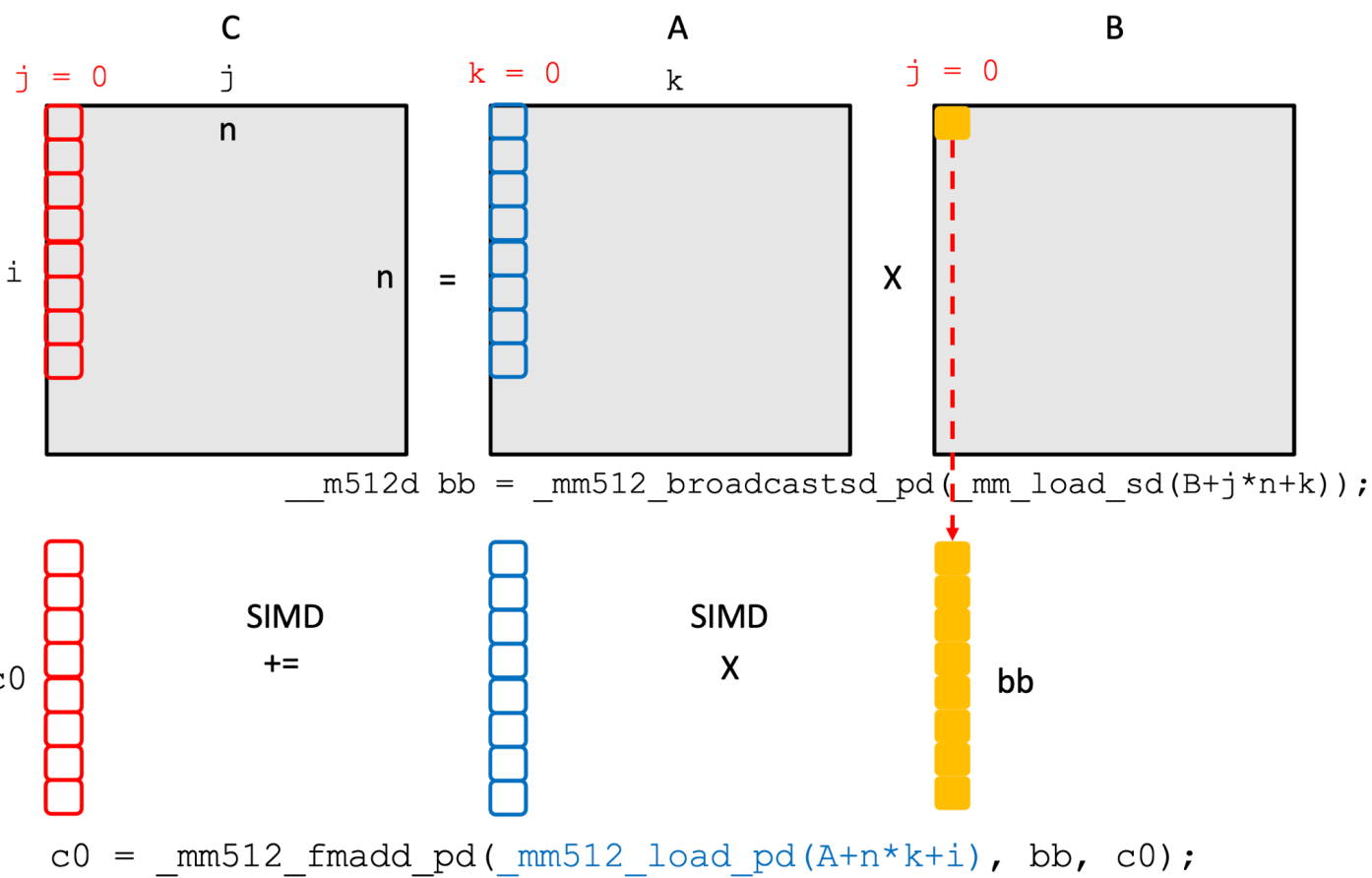
  • 우선 위 그림에서 보다시피 output matrix 인 C 에서 j = 0 을 얻기 위해서는, A matrix 에서 k = 0 ~ K 에 해당하는 각각의 column 에 대해 B matrix 에서 j = 0 에 해당하고 k = 0 ~ K 에 해당하는 값을 모두 곱해서 더해줘야 한다.
  • 이것을 SIMD 연산할 때는, C 의 column vector 에다가 A 의 k = 0 에 대한 column vector, 그리고 B 의 j = 0, k = 0 에 해당하는 값을 채운 vector 두개를 곱한 것을 더해주는 연산을 우선 하게 된다.
    • 여기서 하나의 값을 vector 에 모두 채우는 것은 Broadcast 라고 하고
    • 곱한것을 더하는 것은 FMA 연산이다.

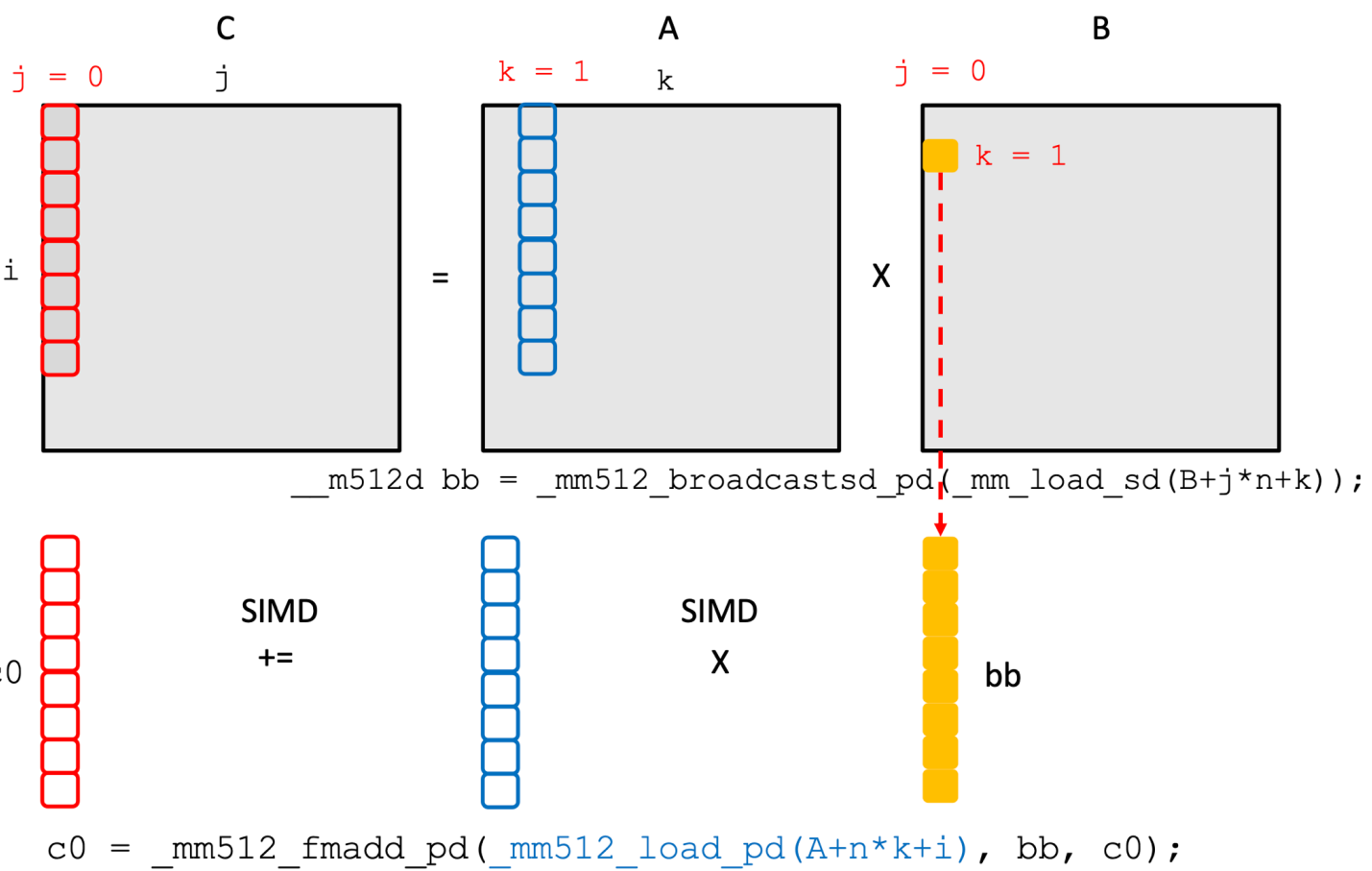
  • 다음에는 C 의 column vector 에다가 A 의 k = 1 에 대한 column vector, 그리고 B 의 j = 0, k = 1 에 해당하는 값을 채운 vector 두개를 곱한 것을 누적하여 더해주게 된다.
  • 그리고 이것을 모든 k 에 대해 반복하면 C 에 대한 column vector 가 계산되는 것.

GPU

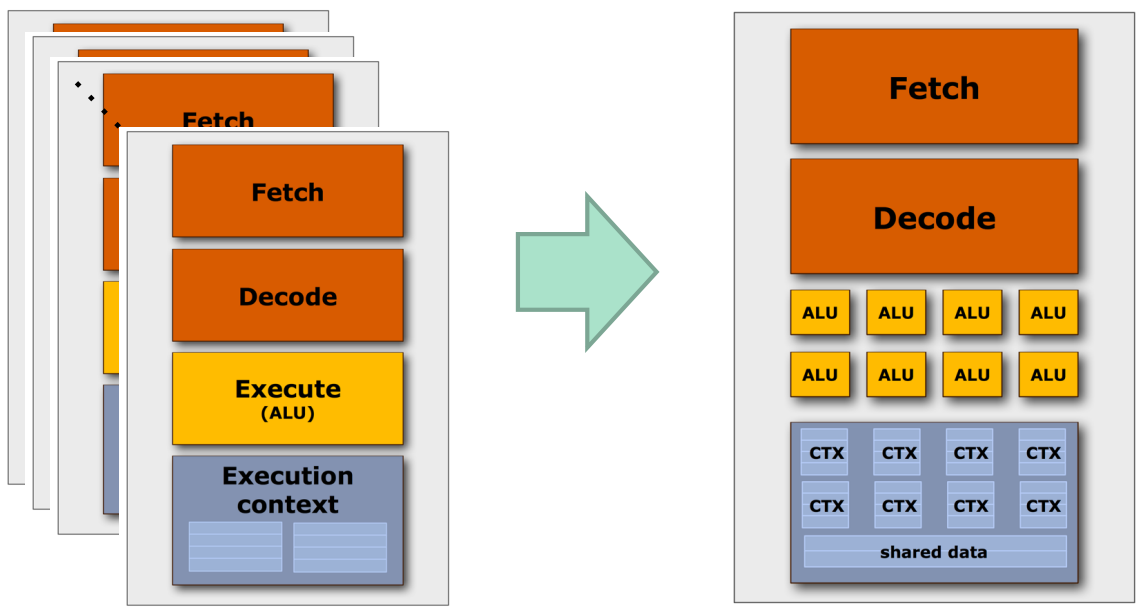
  • SIMD (ISA 그냥 이런 processing pattern) 의 경우에는 instruction 이 모두 동일하기 때문에 이 instruction 을 여러군데에서 fetch-decode 하는 것은 매우 비효율적일 것이다.
    • 따라서 fetch-decode 는 공유하고 경장히 많은 ALU 들과 여기에서 사용할 ctx reg 들이 묶여있는 것이 GPU 의 기본 형태이다.

CUDA Execution Model

  • CUDA 에서 사용하는 execution 과 관련된 용어들을 좀 알아보자.

  • NVIDIA GPU 에서는 하나의 fetch / decode 로 묶인 ALU 및 context register 들을 Streaming Multiprocessor (SM) 이라고 부른다.
  • 그리고 SM 안에서의 각 ALU 는 NVIDIA GPU 에서는 Scalar Processor (SP) 라고 부른다.
    • 즉, 하나의 SIMD lane 인 셈
  • 그리고 이놈들이 실행될때의 실행흐름을 NVIDIA GPU 에서는 Thread 라고 부른다.
  • 하나의 SM 에 “할당” 되는 thread 의 묶음을 NVIDIA GPU 에서는 Thread block 이라고 부른다.
  • 그리고 하나의 GPU device 에 할당되는 thread block 들을 Grid 라고 한다.

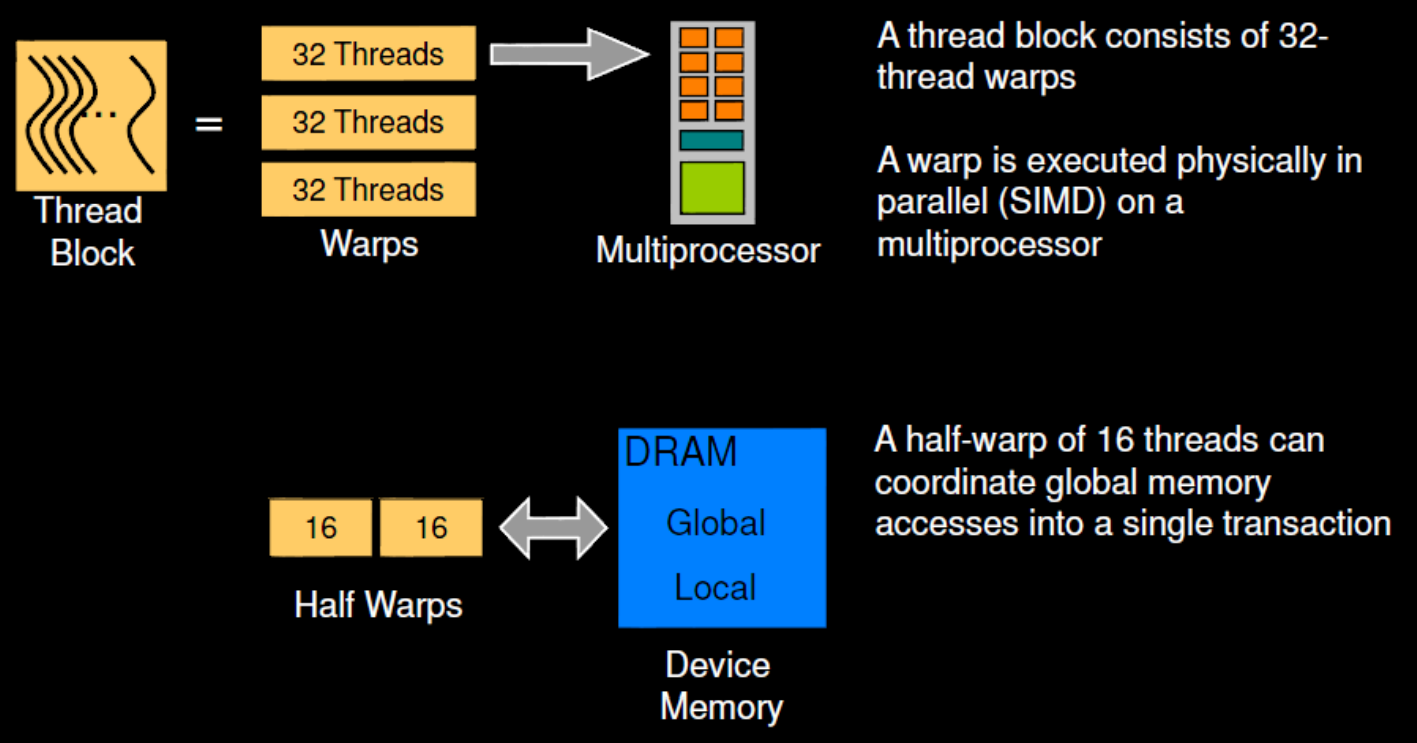
  • SM 에 scheduling 되는 단위가 thread block 이고 SM 에서 실제로 한번에 “실행” 되는 단위는 Warp 이다.
    • 보통 하나의 warp 는 32개의 thread 로 이루어진다.

CUDA Memory Model

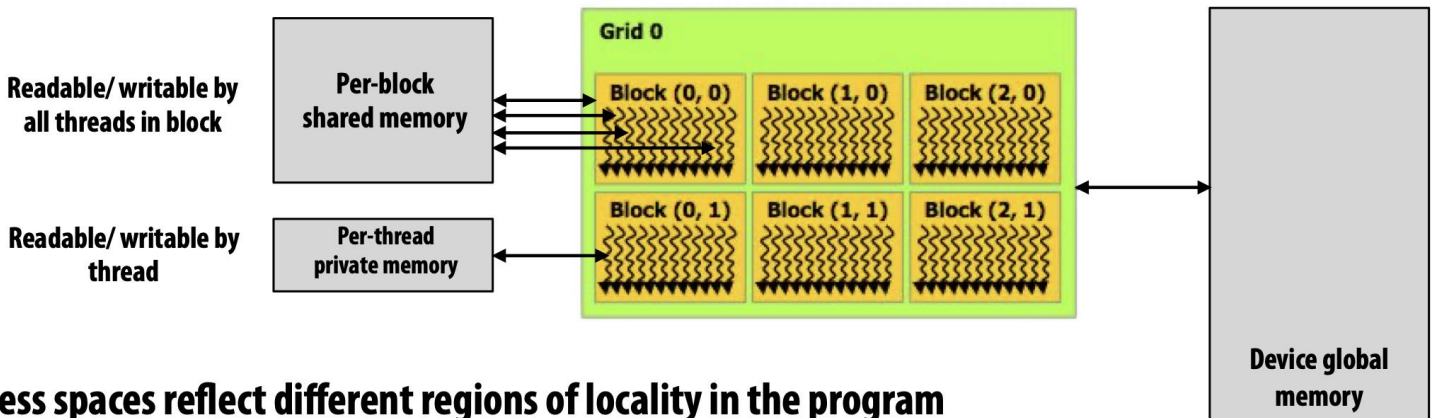
  • Mem hierarchy 의 관점으로는
    • SP 별로 Context register (Per-thread private memory) 가 있고
    • SM 별로는 Local memory (Per-block shared memory) 가 있다.
      • 이 local memory 의 사이즈는 GPU 가 다루는 데이터의 사이즈에 비해서는 아주 작고 따라서 GPU 에서는 보통 cache hit ratio 가 아주 낮다고 한다.
    • 그리고 GPU 에는 Device global memory 가 있다.
      • 여기에 GDDR 혹은 HBM 이 들어간다.
  • 그리고 위 그림에서 볼 수 있다시피 얘네들의 접근 범위가 다르다.
    • Private memory 는 당연히 하나의 thread 에서밖에 접근 못하고
    • Thread block 안에 있는 thread 들은 Local memory 를 공유하고
    • Thread block 간의 thread 들에 대해서는 Global memory 를 공유한다.

Control Divergence (Branch)

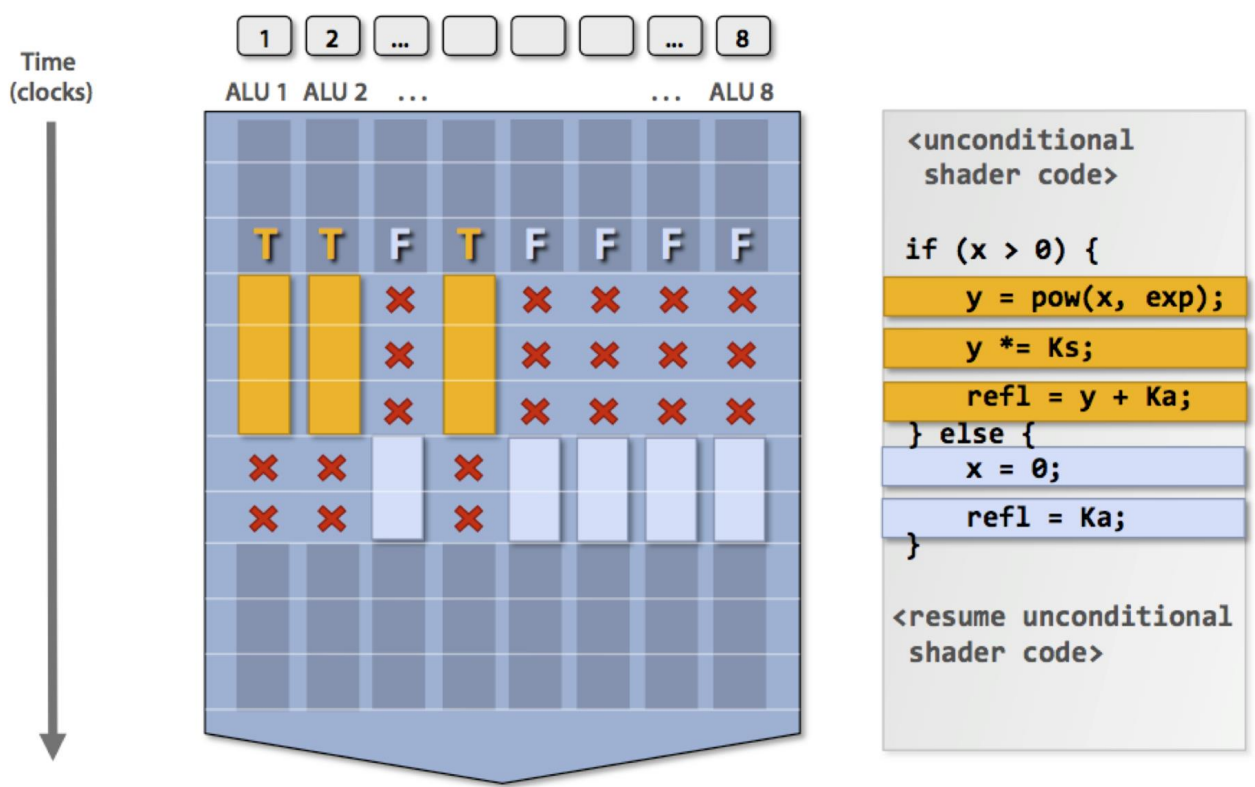
  • GPU 에서의 branch 는 SP 의 일부는 true path 를 따라가고, 나머지 일부는 false path 를 따라간 다음 실제 true 인지 false 인지에 따라 해당 path 의 SP exec result 만 남긴다.
    • 이것이 GPU 에서 기본적으로 Control divergence (즉, branch) 를 처리하는 방법이다.
    • 뭐 이때의 idle cycle 을 최소한으로 하기 위한 여러 논문들이 있지만 그래도 idle cycle 을 아예 회피해버릴 수는 없다고 한다.

Latency Hiding

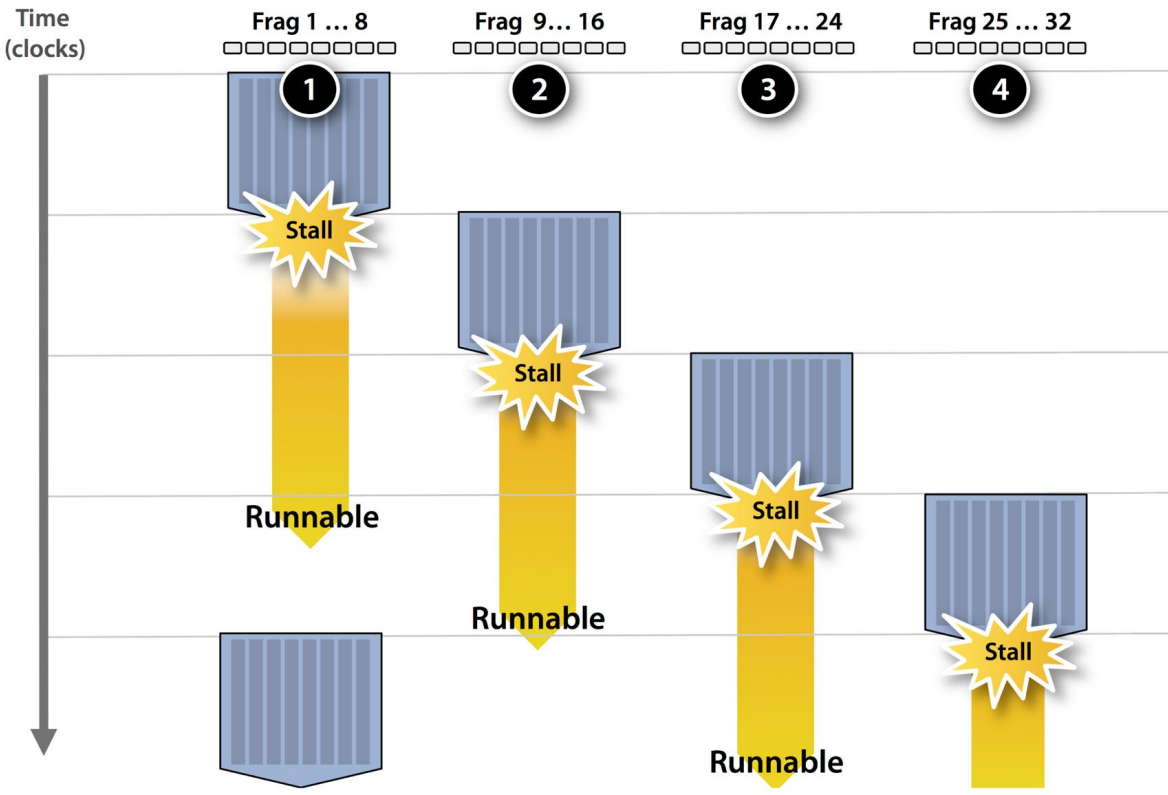
  • SM 안에서는 한 warp 가 mem access 에 의해 stall 이 되면 위 그림처럼 다른 warp 가 돌며 Latency hiding 을 하게 된다.
    • 즉, communication-computation overlapping 하는 것
    • 근데 이러한 방식으로 처리하기 위한 하나의 조건이 있다: 바로 thread 의 수가 충분히 많아야 된다.
      • 즉, thread 의 수가 충분히 많아야 한 warp 가 stall 이 되었을 때 thread block 에서 다른 warp 를 꺼내다가 실행할 수 있게 되는 것이다.
      • 따라서 GPU programming 을 할 때 가장 기본이 되는 것이 thread 가 최대한 많이 돌아갈 수 있게 하는 것이다.

Matrix Addition Example w/ CUDA

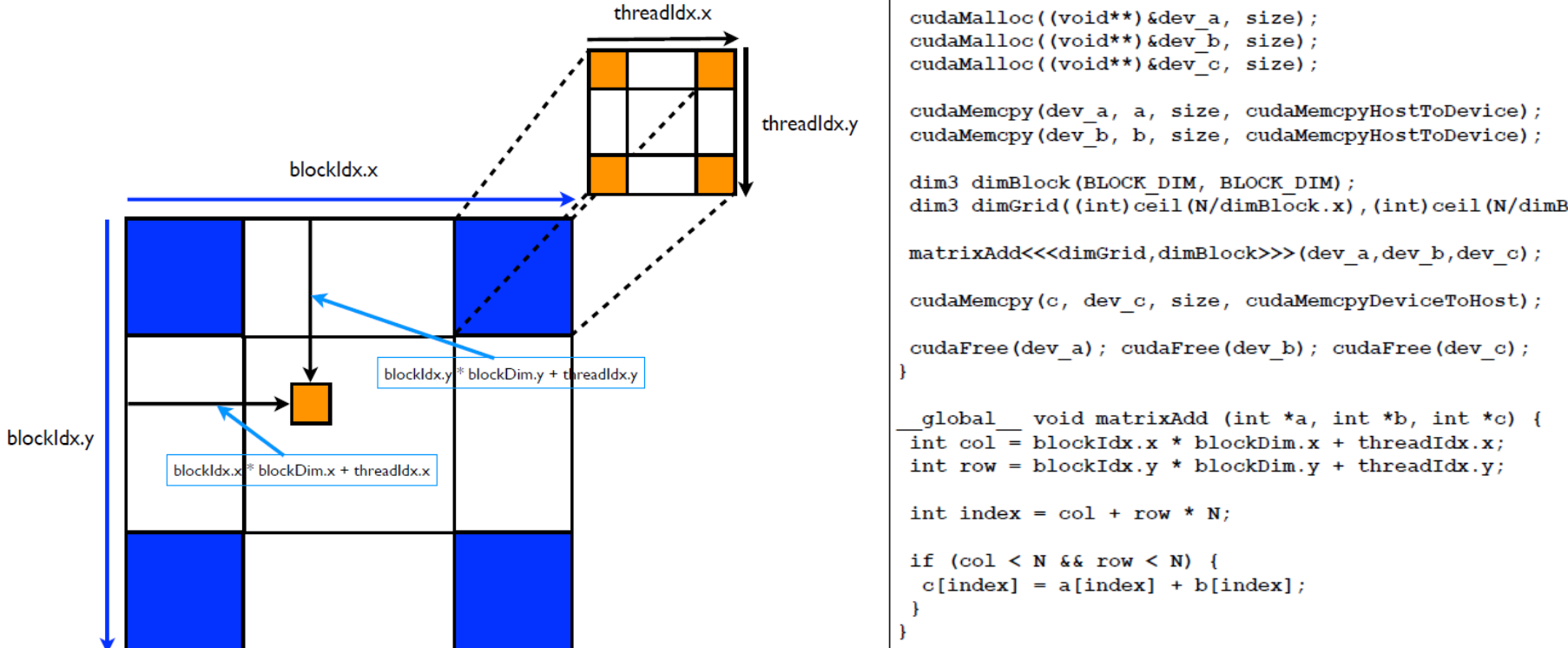
  • 뭐 Matrix addition 자체는 그냥 같은 index 에 위치한 데이터를 그냥 더하면 되는 것이라 별로 어려울 게 없고
  • Kernel code 를 실행하는 각 thread 에 대해, 본인의 위치를 알아내는 방법에 대해 간단하게 알아보자.
    • threadIdx.{x|y|z} 는 thread block 안에서의 본인 thread 에 대한 index 번호 (x, y, z 축 방향으로) 를 알려주는 변수이다.
    • blockIdx.{x|y|z} 는 grid 안에서의 본인 thread 가 속한 thread block 대한 index 번호 (x, y, z 축 방향으로) 를 알려주는 변수이다.
    • blockDim.{x|y|z} thread block 에 대한 (x, y, z 축 방향으로) 크기를 알려주는 변수이다.
  • 그래서 다음과 같이 해주면 grid 안에서의 본인 thread 에 대한 index 번호 (x, y, z 축 방향으로) 를 알 수 있다.
blockDim.{x|y|z} * blockIdx.{x|y|z} + threadIdx.{x|y|z}

Mapped Memory

  • 일반적으로는 GPU memory 에 데이터를 전달해 주기 위해 cudaMalloc 하고 cudaMemcpy 를 쓰는 것이 일반적이다.

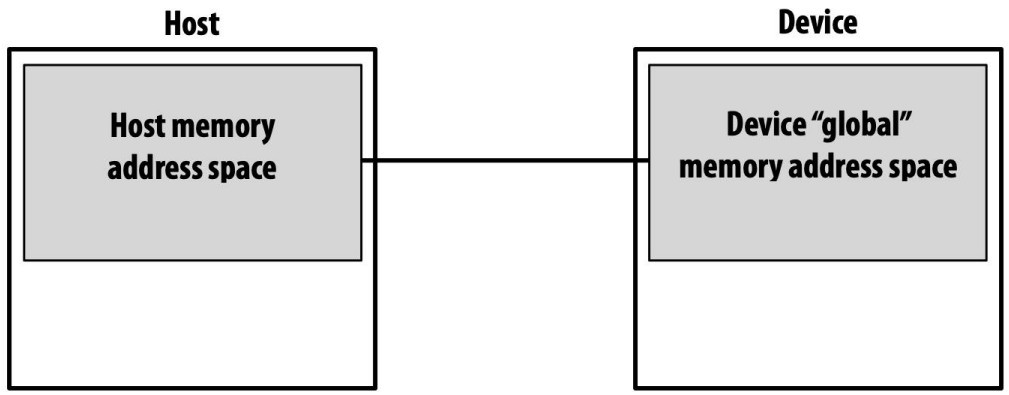
  • 근데 요즘은 Virtual Address Space 에 GPU memory 를 붙여서 code 상에는 그냥 일반적인 변수로 접근을 해도 실행할 때는 자동으로 address translation 을 해서 접근하게 하는 방법 (이런것을 Mapped memory 라고 한다) 이나
  • CUDA Stream 으로 communicate - compute overlapping 을 하는 방식이 많이 사용된다고 한다.

Matrix Multiplication Example

Thread Block Scheduling

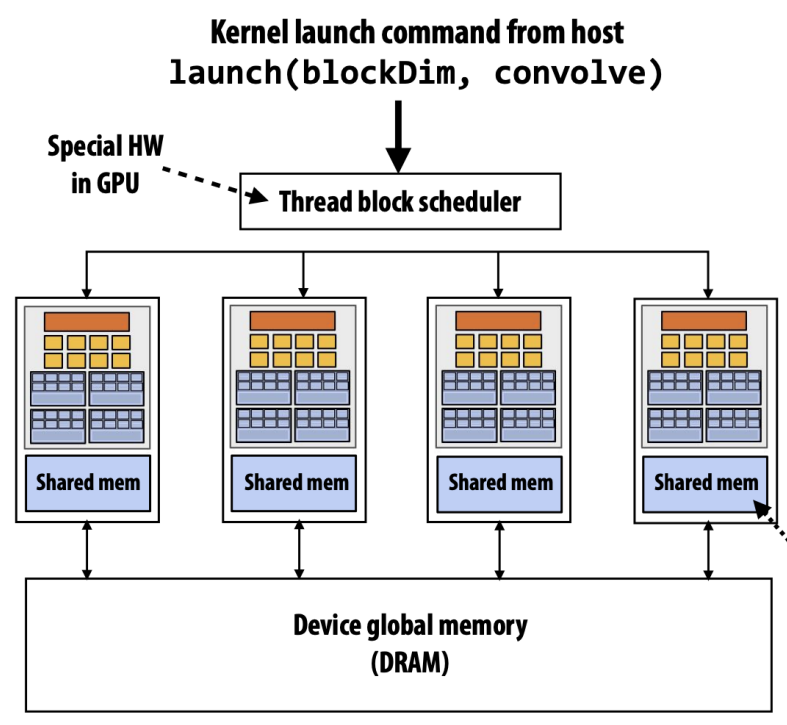
  • Code 를 짤 때는, 내가 갖고 있는 GPU 에 몇개의 SM 이 있는지 등을 알 수 없다.
    • 물론 검색해보면 알 수는 있다. 근데 이런것을 신경쓰지 않게 하는 것이 abstract 자나?
  • 그래서 code 에다가는 Grid 의 크기와 Thread block 의 크기만 알려주면, 그것을 이용해 grid 를 여러개의 thread block 으로 자르고, 각각의 SM 에 할당하는 것은 GPU 내의 Thread block scheduler 가 담당한다.

1D Convolution Example

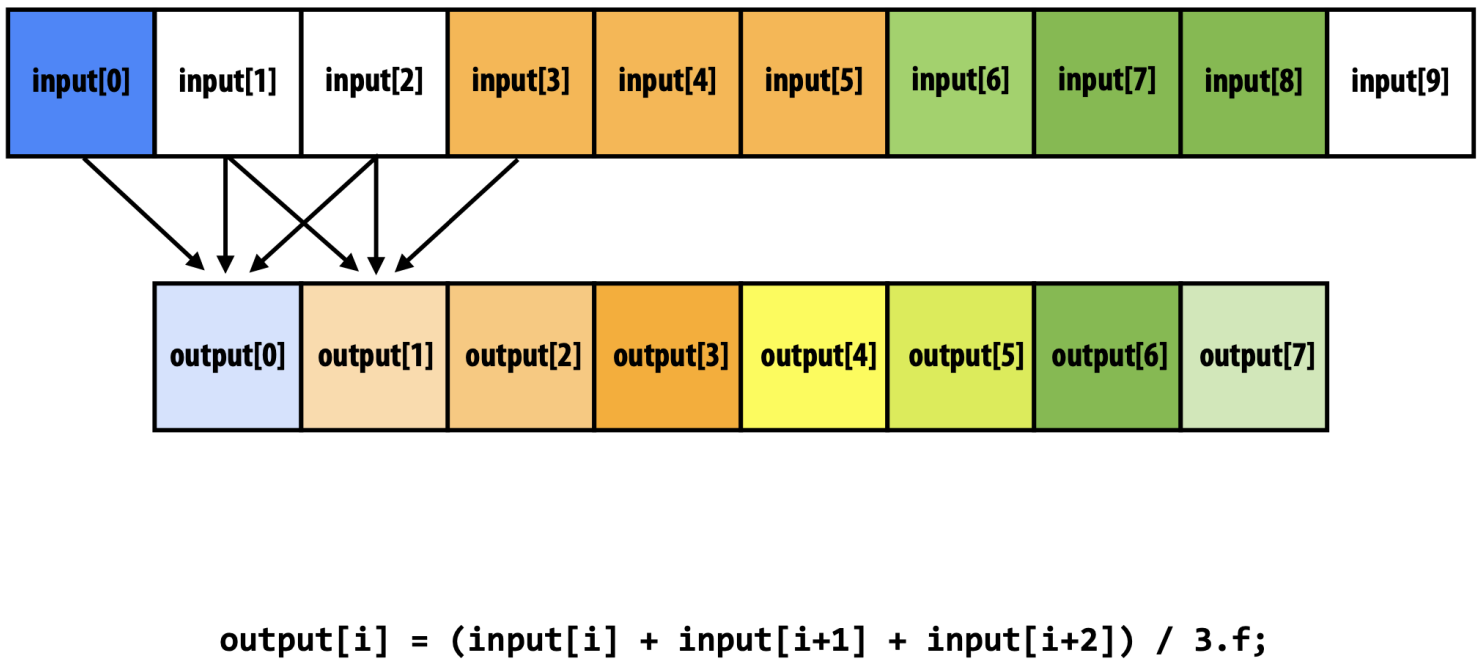
  • 1D convolution 은 input[i] 부터 W (Window size) 개의 input 들을 aggregate 하여 output[i] 을 계산하는 방법이다.
    • 위의 예시는 window size 3 으로 하여 average 를 하는 1D convolution 이다.
  • 이것을 위한 naive version kernel 은 다음과 같다:

  • 보면 일단 간단하기는 한데, 이 코드는 당연히 느리다.
    • 왜냐면 각 thread 가 global memory 인 input[] 에 세번 접근하기 때문.
  • 근데 i 번째 thread 가 output[i] 를 계산하기 위해 input[i], input[i+1], input[i+2] 에 접근하고
    • i+1 번째 thread 는 output[i+1] 를 계산하기 위해 input[i+1], input[i+2], input[i+3] 에 접근한다는 것을 생각해 보면
    • Thread 들이 동일한 데이터에 접근하는데 매번 global memory 에 접근하고 있다는 것을 알 수 있다.
  • 따라서 이것을 방지하기 위해 thread block 이 사용할 데이터를 shared memory 에 일단 다 올려놓고, 여기에 반복적으로 접근하면 훨씬 더 빠르겠다는 생각을 한다.

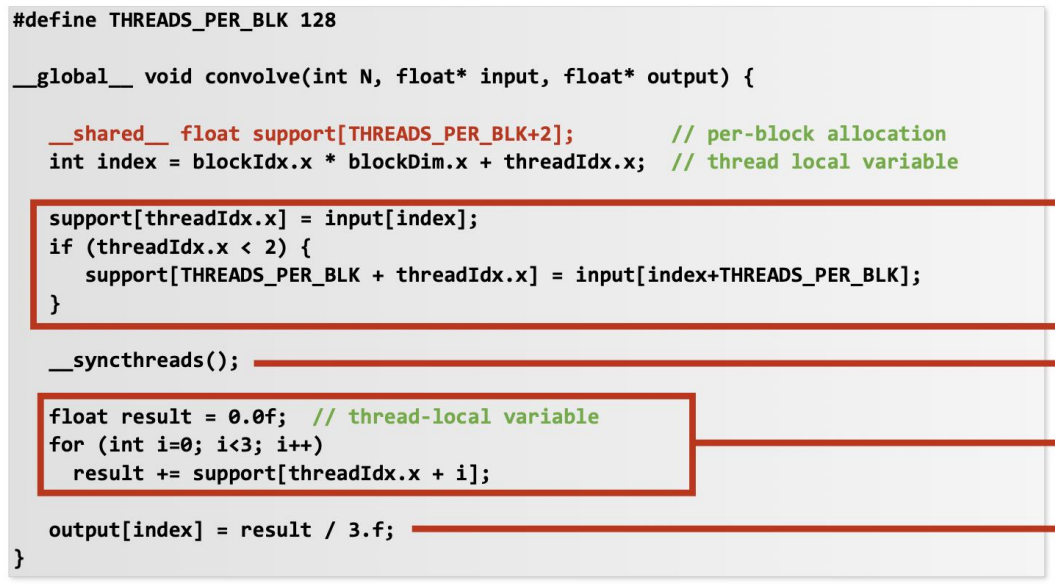
  • 그래서 위의 코드에서는 __shared__ 로 정의된 변수에
    • 우선 input array element 를 하나씩 load 하고
    • __syncthreads() 로 모든 thread 들이 다 load 할 때까지 기다린 다음에
    • 마지막에 naive code 에서처럼 연산해 주게 된다.
  • 이렇게 되면 3 * NUM_THREADS 만큼 global memory 에 접근해야 했던 것이, NUM_THREADS 만큼 접근하게 되면서 훨씬 빨라지게 된다.

Graph View

Backlinks