Madison Digital Garden

Search

SearchSearch

08. 리액턴스

Jan 05, 2025, 12 min read

충남대학교 컴퓨터공학과 남병규 교수님의 "전자회로" 강의를 필기한 내용입니다.

이 문서는 보관이 목적이고, 관리되지 않습니다. 따라서 잘못된 정보가 포함되어 있거나 순서가 뒤죽박죽일 수 있습니다.

AC회로에서의 캐패시터

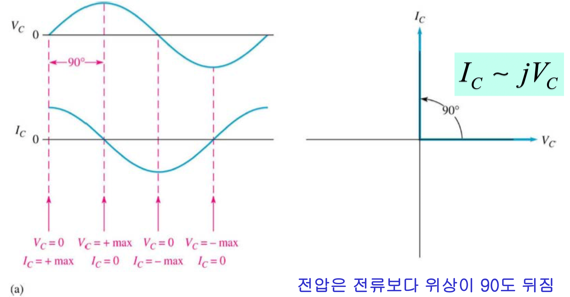
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image1.png

  • 저항과 캐패시터에 나타나는 전압, 전류도 모두 정현파로 나타난다
  • 캐패시터는 전류가 가해져야 전하가 충전돼서 전위가 생길 수 있기 때문에 전류가 전압보다 위상이 90도 앞선다
    • 전류가 점점 줄어들어 0이 되는 구간을 보면 캐패시터가 점점 충전되긴 하지만 전류가 줄어들기 때문에 충전속도도 점점 느려진다
    • 그러다가 전류가 0을 넘어 반대로 흐르게 되면 이것은 캐패시터의 방전시 전류의 방향과 같기 때문에 충전량도 점점 줄어들게 된다
    • 그러다가 전류가 반대방향으로 최대로 흐르는 지점에서는 충전했던 전하가 고갈이 나기 때문에 0이 되었다가
    • 전류가 반대방향으로 계속 흐르기 때문에 캐패시터도 아까와는 반대의 극성으로 충전되게 되는 것
    • 이러한 연유로 캐패시터에 흐르는 전류와 캐패시터의 전압은 90도의 위상차가 생기게 되는 것 이다
    • 전류가 있어야 전압이 있기 때문에 전압이 전류보다 위상이 90도 늦다라고 기억해라
  • 근데 옴의 법칙은 전류와 전압의 위상차가 없는 선형적인 관계일 때 성립하는 등식인데 지금은 위상차가 생기므로 캐패시터가 존재하면 옴의 법칙은 적용되지 않는다
  • 즉, 그냥 dc회로에 저항만 있는 경우에는 v=ir이 성립해 항상 비례관계이지만 이 경우에는 비례관계가 아닌 위상차가 생긴다는 것
  • 따라서 I ~ jV 의 관계가 성립한다 → j는 허수인데 이게 90도 회전한다는 의미를 가지기도 한다
    • j를 두번 곱하면 -1인데 이것을 복소 극좌표계에서 각도의 입장에서 보면 180도 회전이기 때문에 그냥 j는 90도 회전의 의미를 갖게 되는 것

리액턴스

  • 리액턴스(X) : 캐패시터와 인덕터에서 나타나는 AC전류에 의한 반응저항을 의미하며 복소수로 표현되기 때문에 복소저항이라고도 부른다
  • 캐패시터에서는 용량성 리액턴스라고 부르고, 인덕터에서는 유도성 리액턴스라고 한다.
  • 저항과 유사한 역할을 하긴 하지만 저항과는 다음과 같은 차이점이 있다
    • 전류를 소비하지 않고
    • 주파수에 따라 저항값이 달라지고
    • 전압과 전류 사이에 위상차(j)를 발생시킴

용량성 리액턴스

  • 캐패시터에서 발생하는 리액턴스를 용량성 리액턴스(복소저항), 기호로는 Xc로 표기한다

유도과정

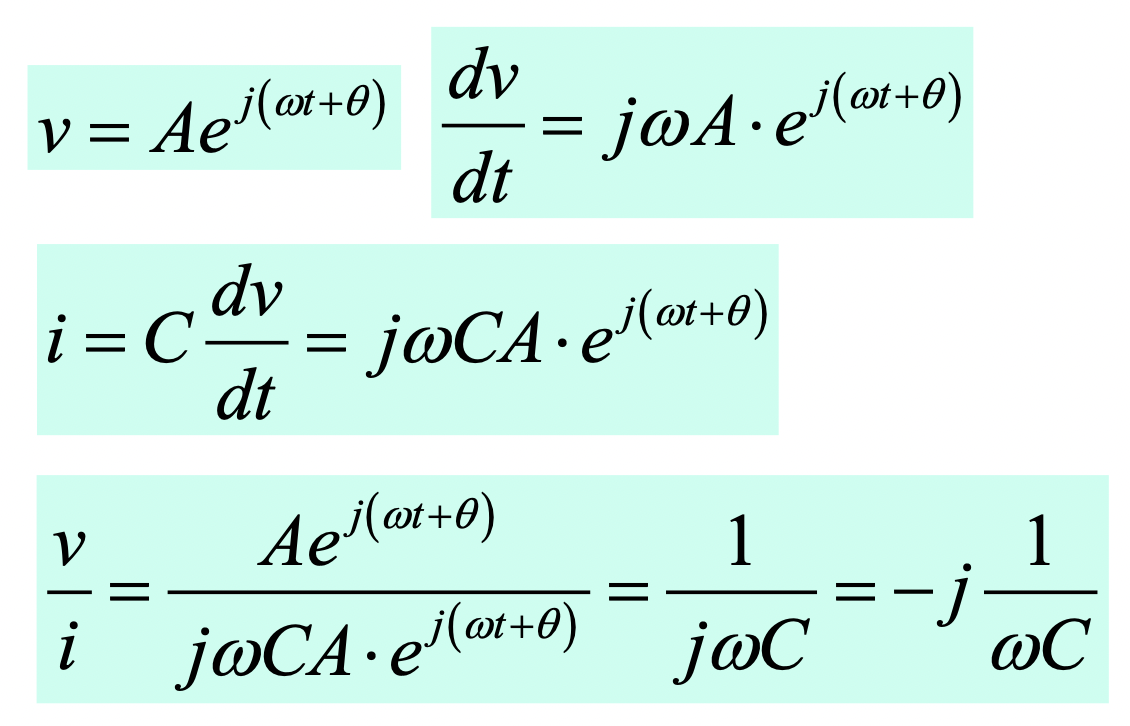
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image2.png

  1. 정현파로 주어지는 전압을 오일러 공식을 이용해 복소수를 이용해 표현한 것을(오일러 공식에는 허수부가 존재하는데 왜 저렇게 표현되는지는 모르겠으나 걍 받아들여라)
  2. t로 미분해 dv / dt 를 구하고
  3. 그것을 이용해 i를 구한 후 - 전류는 캐패시턴스가 클수록, 전압이 빠르게 변할수록 잘 흐른다고 캐패시터 부분에서 말했었쥬?
  4. 옴의 법칙을 이용해 저항을 구해보면
  • 1 / jwc 가 되는데 복소수로 표현된 저항이므로 복소저항, 즉 리액턴스이다
  • 따라서 용량성 리액턴스(Xc) = 1 / jwc 로 표현된다
    • 얘를 의미론적으로 이해해보면 w가 주파수이므로 전압의 주파수가 높다는 것은 결국에는 캐패시터에서 전류를 더 잘 흐르게 하므로 리액턴스인 Xc는 작아지게 되는 것
  • 문제에서 리액턴스의 크기가 주어지면 1 / wc 만 주어진 것 이므로 -j 를 붙여서 위상에 대한 정보까지 추가해서 계산 해야 한다

AC회로에서의 인덕터

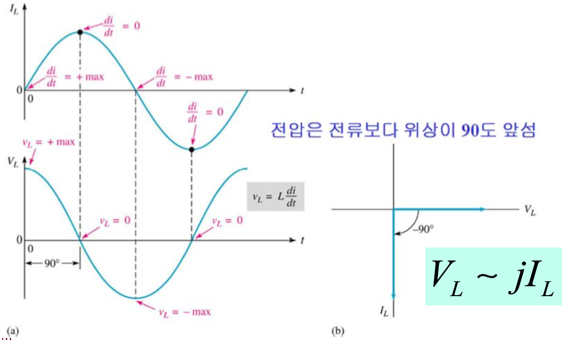
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image3.png

  • 전류의 변화가 클수록 많은 전압이 유도되므로 전류 정현파의 접선의 기울기가 제일 큰 0에서 전압이 제일 많이 유도된다 → 전압이 전류보다 위상이 90도 앞선다 - 꼭 기억할 것!!
    • 캐패시터와 비교해서 캐패시터는 뭐가 앞서고 인덕터는 뭐가 앞서는지 꼭 기억할 것
  • V ~ jI 인 셈이다

유도성 리액턴스

  • 인덕터에서 유도되는 리액턴스를 유도성 리액턴스(복소저항), 기호로는 Xl라고 부른다

유도과정

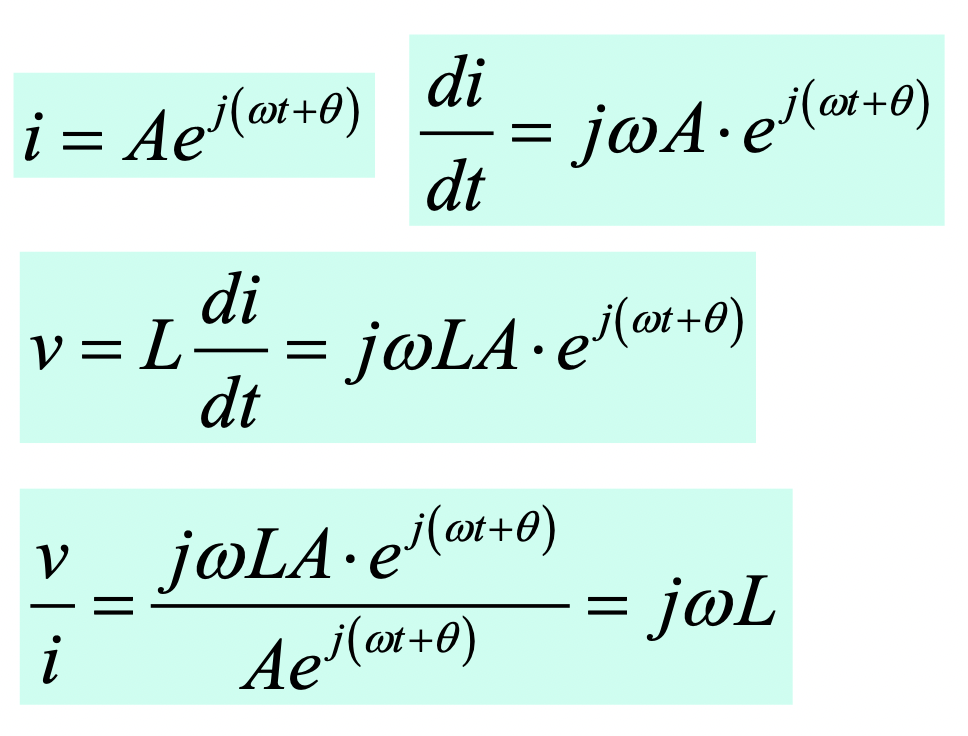
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image4.png

  1. 이번에는 정현파로 주어지는 전류를 오일러 공식을 이용해 복소수로 표현한 것을
  2. 양변을 t로 미분해 di / dt 를 구한다
  3. 그리고 인덕터에서는 전류가 빠르게 변할때 높은 전압이 유도됨을 이용하여 전압에 대한 공식을 유도하고
  4. 마찬가지로 옴의법칙을 이용해 저항을 구해보면
  • 유도성 리액턴스(Xl) = jwL 이 나오게 된다
    • 얘를 의미론적으로 이해해보면 전류의 주파수인 w가 크다는 것은 그만큼 전류가 빠르게 변하는 것이고 그럼 유도전압이 많이 유도되어 전류가 흐르기 힘들어진다. 따라서 Xl이 커지는 것
  • 이때에도 유도성 리액턴스의 크기가~옴으로 주어지면 위상정보인 j를 붙여야 Xl값이 나오게 된다

임피던스

  • 복소저항과 일반저항을 포괄하는 상위개념이 임피던스 이다 - 단위는 그대로 옴을 사용함
  • 임피던스(Z) = 순수저항(R) + 리액턴스(X) * j 즉, 순수저항이 실수부이고 리액턴스가 허수부인 것 이다
  • 따라서 저항과 캐패시터, 인덕터가 섞여있는 회로에서의 임피던스는 얘네를 +, || 를 통해 합성한 후 실수부와 허수부를 나누면 구할 수 있다
  • 교류회로에서 V = IZ 가 성립한다
  • 임피던스 저항의 상위개념이기 때문에 저항처럼 직렬시에는 더해주고 병렬시에는 저항처럼 || 연산을 하면 된다

반대개념들

  • 컨덕턴스(G) : 저항의 역수(옛날에 배웠던 전도도)
  • 서셉턴스(B) : 리액턴스의 역수
  • 어드미턴스(Y) : 임피던스의 역수
  • Y = G + Bj 로 표현된다
  • 어드미턴스에서 Y = G + Bj 를 역수취하면 1 / G + 1 / B 와는 다르다고 생각할 수 있는데 G = R / (R^2 + X^2), B = -X / (R^2 + X^2) 가 성립하기 때문에 같댄다 - 별로 중요한건 아님

교류 회로의 해석

  • 이제부터 모든 값들이 페이저로 제시된다
  • 즉, 전압도 페이저의 형태로(페이저 V), 전류도 페이저로(페이저 I), RLC임피던스도 페이저로(페이저 Z)로 제시된다
  • 하지만 옴의법칙에서 저항만 임피던스로 바꾼 V = IZ 가 성립하고
  • KCL, KVL, 직렬 / 병렬에서의 전류 / 전압 분배 등등이 여전히 성립하기 때문에 얘네들을 이용해 회로를 해석해주면 된다

예제

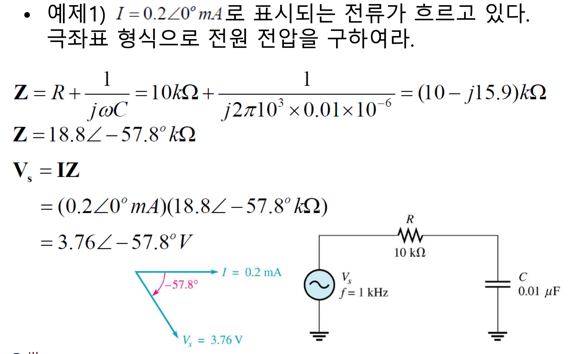
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image5.png

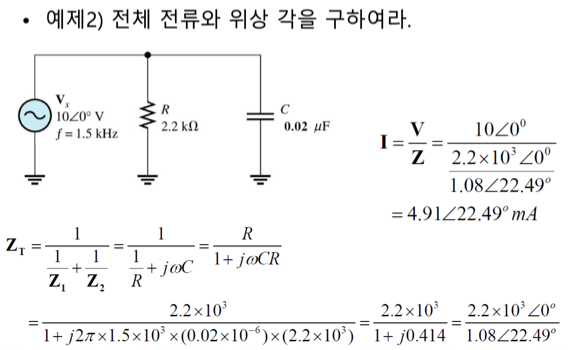
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image6.png

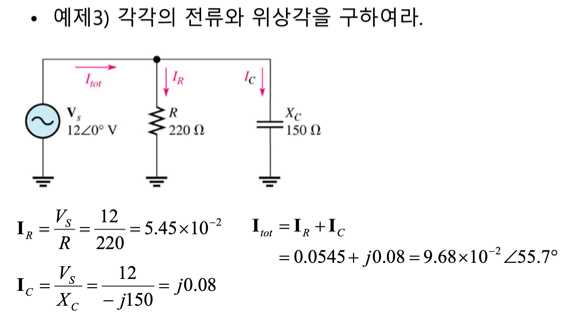
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image7.png

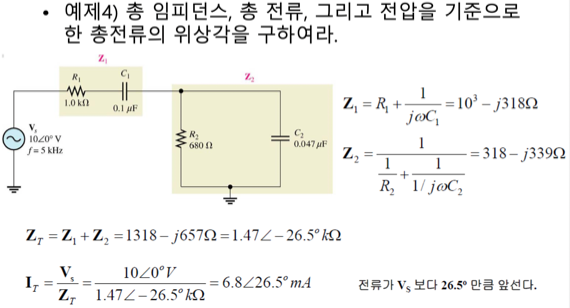
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image8.png

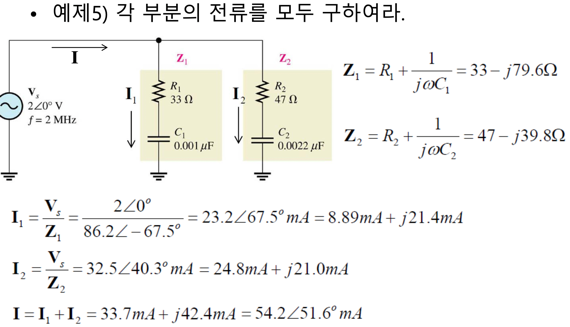
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image9.png

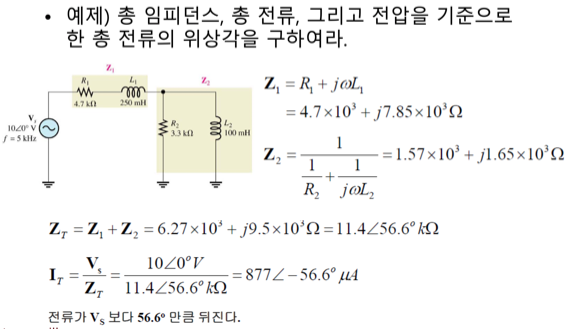
%E1%84%85%E1%85%B5%E1%84%8B%E1%85%A2%E1%86%A8%E1%84%90%E1%85%A5%E1%86%AB%E1%84%89%E1%85%B3%20e8a1b74c19c74b2d91e1da4facad07e5/image10.png

단위환산

  • 나노(-9) → 마이크로(-6) → 밀리(-3) → 0 → 키로(3) → 메가(6) → 기가(9) → 테라(12)

저역 통과 필터

  • 출력포트랑 캐패시터를 병렬로 연결한 후 낮은 주파수의 신호가 들어오면 캐패시터는 DC를 차단하기 때문에 여기로는 전류가 안흐르고 출력포트쪽으로 전류가 흘러 낮은 주파수의 신호를 잡아낼 수 있게 된다
  • 하지만 높은 주파수의 신호가 들어오면 전류가 캐패시터쪽으로 많이 흐르기 때문에 출력으로는 별로 안나와 높은 주파수의 신호를 차단할 수 있게 된다

Graph View

Backlinks