Madison Digital Garden

Search

SearchSearch

06. 인덕터

Jan 05, 2025, 13 min read

충남대학교 컴퓨터공학과 남병규 교수님의 "전자회로" 강의를 필기한 내용입니다.

이 문서는 보관이 목적이고, 관리되지 않습니다. 따라서 잘못된 정보가 포함되어 있거나 순서가 뒤죽박죽일 수 있습니다.

Inductor

  • 한국어로 유도기라고 한다
  • 전류를 자기장 형태로 저장하는 것
  • 전자석처럼 코일형태를 띄고 있다
  • 코일형태로 만들어서 자속(자기장)을 저장하는 것
  • 기억 안나면 인덕션 생각해라 - 인덕션도 코일의 저항을 이용해 열을 발생시키므로 인덕터도 코일처럼 생겼으며 이 코일에 의한 자속으로 전류를 붙잡아두는 것

인덕터의 원리 - 렌츠의 법칙

  • 자속이 전류를 흘러주게 하는 관성과 같은 역할을 해서 전류를 저장할 수 있게 한다
  • 전류를 저장한다는 것은 전류를 유지킨다는 것을 의미한다
  • 전압이 없어져도 자속이 어느정도 남아있으니까 자속이 없어질때까지는 전류가 흐른다는 뜻
  • 자속이 전류의 관성과 같은 놈이므로 전류의 변화가 생기면 그에 대한 저항력을 발생시킨다(전류의 변화에 저항하는 힘을 유도한다고 해서 유도기)
  • 저항이 줄어들어 전류가 커지면 다음과 같은 일이 일어난다
    • 저항이 줄어들면 전류가 높아져야 되는데 이 순간 변화에 대항하기 위해 인덕터의 양단에 전류방향과 반대방향으로 전압이 걸린다
    • 이러면 저항과 인덕터 간의 전위차가 줄어들어서 전류가 높아지지 않는다
    • 하지만 결국에는 에너지를 점점 잃으면서 다시 반발력을 잃고 점점 전류가 증가하게 된다
  • 그리고 반대의 경우로 저항이 높아져 전류가 작아지면 다음과 같은 일이 일어난다
    • 저항을 높여버리면 전류가 줄어야 하는데 인덕터 입장에서는 관성을 유지하기 위해 전류의 방향과 같은 방향으로 전압이 걸린다
    • 따라서 저항과 인덕타 간의 전위차가 커져 전류가 낮아지지 않는다
    • 하지만 마찬가지로 점점 힘을 잃으며 전류가 점차 낮아지게 된다
  • 이렇듯 인덕터를 달면 전류의 변화가 드라마틱하게 일어나지 않고 점진적으로 일어나게 된다
    • 캐패시터랑 반대쥬? 인덕터는 전압의 불연속적인 변화는 가능하지만 전류의 불연속적인 변화는 불가능하다
  • 이러한 전류흐름의 관성을 유지하려고 하는 것을 렌츠의 볍칙이라고 한다

Inductance 수학적으로 계산하기

  • 인덕턴스(유도용량, L) - 전류의 변화에 저항하는 방향으로 전류를 발생시키는 능력 = 자속 저장 능력

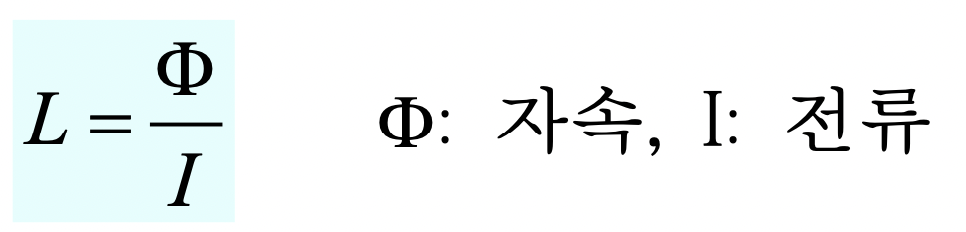
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image1.png

  • 인덕턴스 = 자속의 양 * 전류
    • 전류에 반비례하는 이유는 적은 전류에서는 자속이 추가되는게 더 쉽지만 전류가 큰 경우에는 이미 많은 자속이 들어있기 때문에 자속을 더 추가하는것이 더 힘들기 때문이다
  • 단위는 H(Henry)이다
    • 1H = 1초에 1A의 전류가 변할때 1V의 전압이 유도된다는것

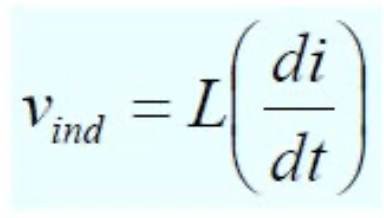
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image2.png

  • 유도전압(Vind) = 유도용량(L) * 전류변화속도(di/dt)

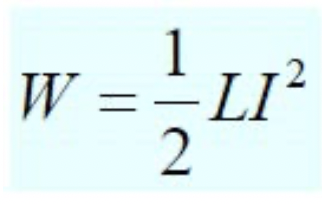
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image3.png

  • 에너지(W)를 전류(I)를 이용해 저장한다

기하구조에 따른 용량

%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image4.png

  • 코일의 길이에 반비례
    • 코일을 촘촘하게 감으면 자기장들이 중첩돼서 더 세어져 더 많은 전류를 저장할 수 있게 된다
    • 따라서 코일에 사용된 도선의 길이가 같을 때 코일의 길이가 길어지면 그만큼 듬성듬성하게 감긴하는 뜻이므로 용량은 줄어들게 됨 - 용수철 길게 늘린거 생각하면 된다
  • 코일단면적에 비례
    • 코일 단면적이 늘어나면 더 많은 자속을 저장할 수 있으므로
  • 권선수의 제곱에 비례 - 권선수는 코일을 감은 횟수를 의미함
    • 코일을 많이 감으면 자속의 갯수 자체도 늘어나고 밀도도 늘어나므로 제곱에 비례하는 거랜다
  • 투자율에 비례
    • 투자율이라는 것은 코일 가운데에 들어있는 물질이 얼마나 잘 자화되는지의 수치이다
    • 즉, 그냥 가운데 있는 물질이 뭐냐에 따라 달라지는 값 - 원자 주변도 전자가 돌기 때문에 이것도 하나의 원자 자석이 될 수 있는데 이것들이 얼마나 주변 자기장에 따라 잘 정렬되는지
    • 정리하면 코일의 가운데에 들어가는 물질이 투자율이 좋아 잘 정렬되면 그만큼 자속이 방해받지 않는 것 이므로 용량도 늘어나게 된다

인덕터의 직렬, 병렬 연결

  • 얘도 걸리는 전압 전류 계산하는 것은 KCL, KVL이용해서 구하면 된다
  • 다만 직렬연결, 병렬연결시에 인덕턴스가 어떻게 변화하는지는 다음과 같다

직렬연결된 인덕터의 인덕턴스

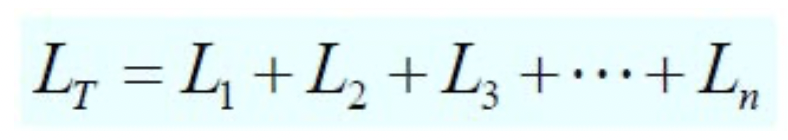
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image5.png

  • 같은 밀도로 코일을 더 감는것과 마찬가지 이므로 자속을 더 저장할 수 있어 인덕턴스가 늘어난다

병렬연결된 인덕터의 인덕턴스

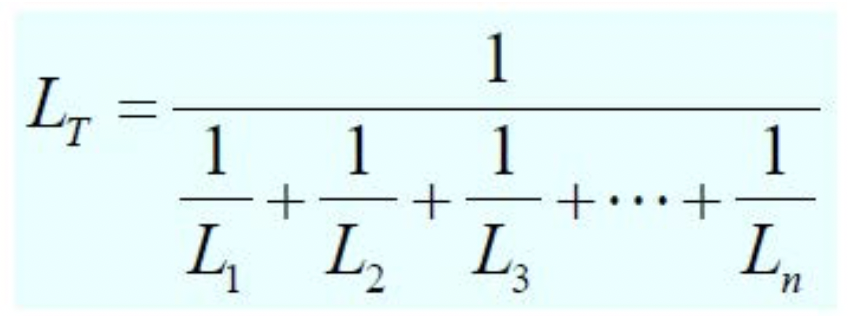
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image6.png

  • 얘는 의미론적으로 이해하기는 좀 어렵다
  • 그냥 병렬 합성 저항처럼 인덕턴스를 계산해주면 된다

정리

  • 인덕터의 합성 인덕턴스 계산은 저항의 합성 저항 구하는 것처럼 생각해주면 된다
    • 즉, 직렬연결하면 인덕턴스도 늘어나고
    • 병렬연결하면 인덕턴스도 줄어든다

정상, 과도상태

  • 렌츠의 법칙에 따라 변화한다
  • 충전될때는 전류의 방향에 반하는 방향으로 전압이 걸려 전류가 서서히 증가한다
    • 단계적으로 알아보면
    1. 먼저 전압을 걸면 일단 인덕터에는 그에 반하는 힘이 바로 유도되어 반대방향으로 같은 전압이 유도된다
    2. 하지만 점차 힘을 잃으며 전압이 점차 낮아지다가
    3. 정상상태에 들어가면 유도전압이 0으로 떨어지게 된다
  • 방전시에는 원래의 전류 방향으로 전압을 걸어 전류를 계속 흘려줘 전류가 서서히 감소한다
    • 이것도 단계적으로 알아보면
    1. 일단 전압을 해제하면 인덕터에는 그에 반하는 힘이 바로 유도되어 같은방향으로 같은 전압이 유도된다
    2. 하지만 점차 힘을 잃으며 전압이 낮아지다가
    3. 유도전압이 0으로 떨어지면 그제서야 전류가 흐르지 않게 되는 것
  • 따라서 인덕터는 dc를 흘리고 ac를 차단한다 - 인덕터는 변화를 싫어하므로 ac를 차단하게 된다

인덕터의 개방법

  • 인덕터가 있을 때 회로를 급작스럽게 단선시켜버리면 인덕터에 반대의 전압이 걸리기 때문에 단선된 부분에 공기를 통해 전류가 흐르게 되어 스파크가 일어난다
  • 이러한 위험한 상황을 피하기 위해서는 인덕터가 발생시키는 전압에 의한 전류를 흐를 수 있도록 백도어를 하나 만들어 주는게 중요하다
    • 하나의 도선을 인덕터와 병렬적으로 연결한 다음 회로를 단선시키면 연결한 도선으로 전류가 흐르며 점차 방전되게 된다

충전, 방전시에의 수식적 해석

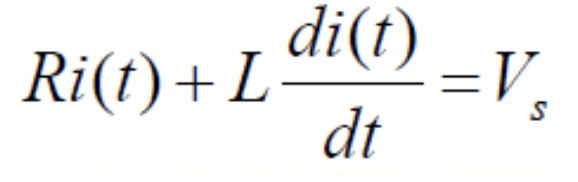
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image7.png

  • 이 공식 외워놔라
  • KVL에 의해 저항에 걸리는 전압과 인덕터에 유도된 전압을 더하면 원래의 전압이 됨
    • 저 Ri(t) 는 R * I(t) 로 옴의 법칙에 의해 저항에 걸린 전압과 같다
    • 그 뒤에 L어쩌고는 위에서 나온 인덕턴스 * 전류변화 속도 이므로 Vind즉, 유도전압을 의미하는 것을 알 수 있다
  • 충전될 때에는 저 Vs에 전원의 전압을 넣어줘서 풀면 되는거고 방전될때는 Vs에 0을 넣어줘서 풀면 되는거다 - 방전될때는 전압이 걸리지 않으므로
  • 풀어보면 충전시에는 I(t) 가

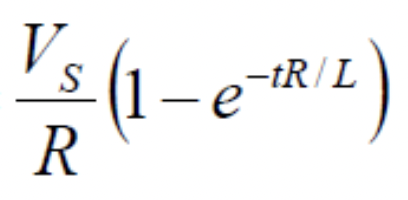
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image8.png

  • 방전시에는

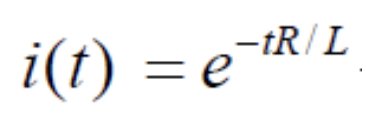
%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image9.png

RL 시정수

%E1%84%8B%E1%85%B5%E1%86%AB%E1%84%83%E1%85%A5%E1%86%A8%E1%84%90%E1%85%A5%205eaa007ea2bc4e1bb4184c39919f4632/image10.png

  • RL 시정수는 전류가 얼마나 잘 변화하는지를 나타내는 상수이다
  • 계산은 타우(t) = 자연발생 저항(R) / 자연발생 인덕턴스(L) 로 한다
  • RC 시정수와 마찬가지로 타우(t) 로 표기한다
  • 이 시정수가 작으면 변화가 잘 일어나지 않고
  • 크면 변화가 빠르게 일어난다

실제에서의 자연적인 요소

  • 사실 인덕터는 회로에서 많이 마주치기가 힘들다 - 캐패시터와 마찬가지로 코일을 감지 않더라도 도선에서 인덕터가 자연적으로 발생하게 된다
  • 하지만 아주 빠르게 변화하는 칩이거나 아주 사이즈가 큰 보드가 아니라면 이 인덕턴스는 잘 보이지 않는다
  • 보통 전자회로를 만들때 자연적으로 발생하는 방해요소는 저항(R) 과 캐패시터(C) 두가지를 주로 고려하게 된다

Graph View

Backlinks